Виведення рівняння теплопровідності для нерухомих тіл
Аналітичне вивчення процесів теплопровідності неможливе без встановлення залежності між фізичними величинами, які характеризують ці процеси і є функціями просторових координат і часу. Математичне вираження цієї залежності, що має форму диференціального рівняння, називають основним диференціальним рівнянням теплопровідності. Воно характеризує протікання процесу теплопровідності в будь-якій точці тіла в будь-який момент часу і дає залежність між температурою, часом і координатами довільного елементарного об’єму. Диференціальне рівняння теплопровідності є наслідком закону збереження енергії і закону теплопровідності Фур'є. Припустимо, що розглянуте тіло нерухоме, процес теплопровідності нестаціонарний, а температурні деформації елементарного об’єму дуже малі в порівнянні з об’ємом. Розглянемо нескінченно малий об’єм dx dy dz у прямокутній системі координат Oxyz (Рис.1). Через грань dydz до поверхні елементарного об’єму за час dt уздовж осі Ox підводиться кількість теплоти dQx, що визначається рівністю dQx = qx× dy× dz× dt (1) Через протилежну грань x + dx відводиться кількість теплоти dQx+dx = dQx +
Підрахуємо різницю між кількістю теплоти, підведеної за рахунок теплопровідності до елементарного об’єму за час dt уздовж осі Ох і кількістю теплоти, відведеної від нього за цей же час уздовж осі Ох:
dQx - dQx +dx = -
Рисунок 1– Схема до виведення диференціального рівняння теплопровідності
Аналогічним чином записується зміна кількості теплоти уздовж осей Oy, Oz dQy - dQy +dy = - dQz - dQx + dz = - Склавши рівності (3) і (4), одержимо різницю між загальною кількістю підведеної і відведеної теплопровідністю теплоти за час dt через поверхню елементарного об’єму: dQ1 = - Отже, до елементарного об’єму за час dt, підведена за рахунок теплопровідності кількість теплоти dQ1, яка обумовлена рівністю (5). Усередині тіла може виділятися чи поглинатися теплота в результаті, наприклад, хімічних перетворень, випаровування вологи, дії електричного струму та інше. Тобто в тілі можлива наявність об'ємних джерел (стоків) теплоти. Позначимо qv потужність внутрішніх джерел теплоти (її ще називають об'ємною густиною теплового потоку), що визначається як кількість теплоти, яка виділяється (поглинається) внутрішніми джерелами (стоками) за одиницю часу в одиниці елементарного об’єму середовища. Припустимо, що qv є відома функція координат і часу qv=qv(x, y, z, t), тоді кількість теплоти, виділена в елементарному об’ємі внутрішніми джерелами теплоти за час dt dQ2 = qv× dx× dy× dz× dt (6) Акумульована в елементарному об’ємі за рахунок теплопровідності теплота dQ1, а також виділена об'ємними джерелами теплота dQ2, відповідно до закону збереження енергії, витрачається на збільшення внутрішньої енергії dQ1 + dQ2 = d при ізобарному процесі (p = const) dQ1 + dQ2 = dH (8) Вважаючи внутрішню енергію одиниці об'єму функцією об’єму і температури, одержуємо
де r - густина речовини, кг/м3; Сv – ізохорна теплоємність одиниці об'єму, Дж/м3× К. Підставляючи вираз для
Оскільки
У випадку ізобарного процесу, розглядаючи ентальпію одиниці об'єму Н як функцію температури і тиску, можна одержати:
де Ср – ізобарна теплоємність одиниця об'єму Дж/(м3× К); Підставляючи (12) у (7) і використовуючи рівності (5), (6), одержуємо:
Вираз (11), (13) є диференціальними рівняннями енергії відповідно для ізохорного та ізобарного процесів. Для твердих тіл Cv× чи при l = const:
Рівняння (15) називають диференціальним рівняннямтеплопровідності. Воно встановлює зв'язок між зміною температури будь-якої точки тіла в просторі і часі. При виведенні рівняння (15) була використана декартова система координат, а елементарний об’єм вибирали у формі паралелепіпеда. Однак можна одержати диференціальне рівняння теплопровідності більш загальним способом у довільній системі координат, використовуючи формулу Остроградського-Гаусса. Виділимо в деякому середовищі, де здійснюється процес теплопровідності, довільний об’єм V, обмежений поверхнею S. Кількість теплоти, що проходить в одиницю часу через поверхню S, відповідно до закону Фур'є dQ1 = - l× grad TdS (16) За рахунок внутрішніх джерел виділиться кількість теплоти dQ2 = Теплота, акумульована теплопровідністю і виділена внутрішніми джерелами в одиницю часу, викликає зміну внутрішньої енергії об’єму V на величину d Відповідно до закону збереження енергії dQ1 + dQ2 = d чи відповідно до формул (16) – (18)
Перетворимо поверхневий інтеграл у правій частині рівності (19) в інтеграл за об'ємом, використовуючи формулу Остроградського-Гаусса:
Тоді рівняння (19) прийме вигляд
У силу довільного вибору об’єму V, з (12) витікає рівняння
яке є найбільш загальною формою запису основного диференціального рівняння теплопровідності. При цьому передбачається, що l, CV, qv можуть бути довільними функції температури чи координат і часу. У багатьох практичних випадках теплопровідність мало залежить від температури і її можна вважати постійною. Тоді рівняння (22) значно спроститься
Коефіцієнт пропорційності в рівнянні (23) Можна надати температуропроводності Одним з найбільш теплоінерційних тіл є вода, її температуропроводність при T = 363 К та тиску P = 0, 1 МПа дорівнює:
Гази володіють малою тепловою інерцією, наприклад, для повітря за тих самих умов
Температуропроводність, так само як l і Сv залежить від температури, а температуропроводність пористих і порошкоподібних тіл – від щільності і вологості. Однак для ряду задач у першому наближенні можна вважати
|

 … (2)
… (2) (qx)× dx× dy× dz× dt (3)
(qx)× dx× dy× dz× dt (3)
 (qy)× dx× dy× dz × dt,
(qy)× dx× dy× dz × dt, (qz)× dx× dy× dz× dt (4)
(qz)× dx× dy× dz× dt (4) (5)
(5)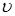 , якщо процес протікає при постійному об’ємі V, або на збільшення ентальпії Н, якщо процес протікає при постійному тиску. Складемо рівняння теплового балансу за час dt для елементарного об’єму dxdydz в кожному з цих випадків: при ізохорному процесі (V = const).
, якщо процес протікає при постійному об’ємі V, або на збільшення ентальпії Н, якщо процес протікає при постійному тиску. Складемо рівняння теплового балансу за час dt для елементарного об’єму dxdydz в кожному з цих випадків: при ізохорному процесі (V = const).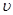 ; (7)
; (7) = Cv×
= Cv×  , (9)
, (9) - ізохорна теплоємність одиниці маси, Дж/кг× К;
- ізохорна теплоємність одиниці маси, Дж/кг× К;
 (10)
(10) qx/
qx/ 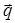 , перепишемо (10) у вигляді
, перепишемо (10) у вигляді (11)
(11) (12)
(12) - ізобарна теплоємність одиниці маси, Дж/(кг× К);
- ізобарна теплоємність одиниці маси, Дж/(кг× К); (13)
(13) близькі, тому можна прийняти
близькі, тому можна прийняти  . Величину Сv називають ще об'ємноютеплоємністю. Використовуючи закон Фур'є, запишемо рівняння (13) у вигляді:
. Величину Сv називають ще об'ємноютеплоємністю. Використовуючи закон Фур'є, запишемо рівняння (13) у вигляді: (14)
(14) (15)
(15) (17)
(17) (18)
(18) (19)
(19) (20)
(20)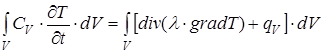 (21)
(21) , (22)
, (22) (23)
(23) називається температуропровідністю і виміряється в м2/с. Зупинимося на фізичному змісті температуропроводності. Можна показати, що
називається температуропровідністю і виміряється в м2/с. Зупинимося на фізичному змісті температуропроводності. Можна показати, що  дорівнює кількості теплоти, яка протікає в одиницю часу через одиницю поверхні при перепаді об'ємної концентрації внутрішньої енергії або ентальпії в 1 Дж/м3 на одиницю довжини нормалі, тобто температуропроводність є коефіцієнтом дифузії внутрішньої енергії при V = const чи ентальпії при Р = const. У зв'язку з чим розрізняють температуропроводність при постійному об’ємі
дорівнює кількості теплоти, яка протікає в одиницю часу через одиницю поверхні при перепаді об'ємної концентрації внутрішньої енергії або ентальпії в 1 Дж/м3 на одиницю довжини нормалі, тобто температуропроводність є коефіцієнтом дифузії внутрішньої енергії при V = const чи ентальпії при Р = const. У зв'язку з чим розрізняють температуропроводність при постійному об’ємі  і температуропроводність при постійному тиску
і температуропроводність при постійному тиску  . Для твердих тіл
. Для твердих тіл 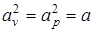 2.
2. прямо пропорційна величині
прямо пропорційна величині  , характеризує інерційні властивості тіла у відношенні поширення температурного поля.
, характеризує інерційні властивості тіла у відношенні поширення температурного поля.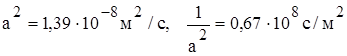 .
.



