Непрерывные проценты
В практических финансово-кредитных операциях непрерывное наращение, т.е. наращение за бесконечно малые отрезки времени, применяется редко. Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например при обосновании и выборе инвестиционных решений, в финансовом проектировании. С помощью непрерывных процентов удается учесть сложные закономерности процесса наращения, например, использовать изменяющиеся по определенному закону процентные ставки. При непрерывном наращении процентов применяют особый вид процентной ставки – силу роста (force of interest). Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени. Постоянная сила роста. При дискретном начислении процентов m раз в году по номинальной ставке наращения r наращенная сумма находится как
Чем больше
где e – основание натуральных логарифмов. Для того, чтобы отличать непрерывную ставку от дискретной, обозначим силу роста как δ. Тогда можно записать
Сила роста представляет собой номинальную ставку сложных процентов при
следует:
Дисконтный множитель на основе силы роста можно определить из
Дисконтный множитель равен
|
, тем меньше промежуток между моментами начисления процентов. В пределе при 
имеем
:
.
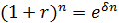
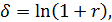
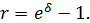
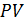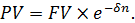
