Примеры 36–3736. В примере 2 §2 доказывается, что при ортогональном проектировании на плоскость XOY векторов пространства Ез (которое является эпиморфизмом) нуль-вектор 37. В примере 3 §2, показано, что: во-первых отображениеh: R
является изоморфизмом, а во-вторых, что при этом единица алгебры R ОПРЕДЕЛЕНИЕ 12. Алгебра A = (А; По-другому моноид - это полугруппа A = (А; е) с выделенным нейтральным элементом. Любая подалгебра моноида называется подмоноидом. Подмоноид всегда является полугруппой с нейтральным элементом. 6°. Если существует нейтральный элемент е относительно бинарной операции Но может случиться, что индуцированная бинарная операция */ А на обладает A
|
из Ез переходит в нуль - вектор 
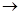R, определяемое правилом
.
переходит в нуль алгебры R 
.
, е) типа (2, 0) с ассоциативной бинарной операцией 
- подмножество множества А, содержащее е, то е является нейтральным элементом относительно бинарной операции */A 
