1°. Если во множестве А с бинарной операцией  существует нейтральный элемент е, тоон единственный.
существует нейтральный элемент е, тоон единственный.
Доказательство. Пусть во множестве А существуют два нейтральных элемента e  и е
и е 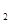 относительно бинарной операции
относительно бинарной операции  . Тогда согласно определению 11 выполняются условия
. Тогда согласно определению 11 выполняются условия
 , (7)
, (7)
 . (8)
. (8)
В частности, при х =  и х =
и х =  соответственно в (7) и (8) получаем
соответственно в (7) и (8) получаем
 .
.
Отсюда из равенства левых и средних частей получаем  .
.
ч.т.д.
2°. Если во множестве А с бинарной операцией  существует нейтральный элемент е, то все левые и правые нейтральные элементы совпадают с ним.
существует нейтральный элемент е, то все левые и правые нейтральные элементы совпадают с ним.
Доказательство. Это свойство является непосредственным следствием свойства 1°.
ч.т.д.
3°. Нейтральный элемент е относительно бинарной операции  на множестве А является центральным элементом относительно бинарной операции
на множестве А является центральным элементом относительно бинарной операции  .
.
Доказательство. Свойство 3° следует из определений центрального и нейтрального элементов (условия для определений одни и те же относительно элемента е).
ч.т.д.
4°(5°). При гомоморфизме (изоморфизме) h: А 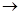 А' алгебры A = (А;
А' алгебры A = (А;  , е) в (на) однотипную алгебру A ' = (А';
, е) в (на) однотипную алгебру A ' = (А';  , е') нейтральный элемент е, относительно бинарной операции
, е') нейтральный элемент е, относительно бинарной операции  переходит в нейтральный элементе' относительно бинарной операции
переходит в нейтральный элементе' относительно бинарной операции  .
.
Доказательство. Пусть при гомоморфизме (изоморфизме) h алгебры A = (А; е) в (на) однотипную алгебру A '=(А ';  , е') элемент х переходит в элемент х', а нейтральный элемент е, относительно бинарной операции
, е') элемент х переходит в элемент х', а нейтральный элемент е, относительно бинарной операции  на А переходит в элемент h (e) = е' множества A '. Покажем, что h (e) = е' -нейтральный элемент относительно бинарной операции
на А переходит в элемент h (e) = е' множества A '. Покажем, что h (e) = е' -нейтральный элемент относительно бинарной операции  на А '.
на А '.
Учитывая то, что h - гомоморфизм (изоморфизм), а е - нейтральный элемент, имеем
 .
.
или  то есть элемент h (е)= е ' - нейтральный элемент относительно бинарной операции
то есть элемент h (е)= е ' - нейтральный элемент относительно бинарной операции  на А.
на А.
ч.т.д.

 существует нейтральный элемент е, тоон единственный.
существует нейтральный элемент е, тоон единственный. и е
и е 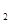 относительно бинарной операции
относительно бинарной операции  , (7)
, (7) . (8)
. (8) и х =
и х =  соответственно в (7) и (8) получаем
соответственно в (7) и (8) получаем .
. .
.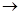 А' алгебры A = (А;
А' алгебры A = (А;  .
. то есть элемент h (е)= е ' - нейтральный элемент относительно бинарной операции
то есть элемент h (е)= е ' - нейтральный элемент относительно бинарной операции 


