Примеры 25–30
25. Для бинарных операций сложения и умножения на мно- жестве N обратные им операции вычитания и деления невыполнимы. 26. Бинарная операция сложения на Z, Q, R- обратимая. 27. Бинарная операция умножения на , Z, Q, R -необратимая. 28. Бинарная операция умножения на – Q *= Q\{0}, R*=R\{0} - обратимая. 29. Сложения матриц на М
30. Умножение матриц на М
Уравнение А× Х=В равносильно следующему уравнению X=A п.4. Нейтральный элемент. ОПРЕДЕЛЕНИЕ 9. Элемент e e ОПРЕДЕЛЕНИЕ 10. Элемент е x ОПРЕДЕЛЕНИЕ 11. Элемент е из А называется нейтральным относительно бинарной операции e Нейтральный элемент аддитивно записываемой бинарной операции называется нулевым или нулем (или началом) и обозначается через 0 (если только это не сопряжено с риском смешения с натуральным числом 0). При мультипликативной записи бинарной операции нейтральный элемент называется единичным или единицей и обозначается просто через 1 (если нет опасности путаницы с натуральным числом 1).
|

 является обратимой операцией, так как
является обратимой операцией, так как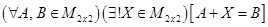


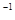 × B, а A
× B, а A  .
. из А называется левым нейтральным элементом относительно бинарной операции если для любого элемента х из А выполняется условие
из А называется левым нейтральным элементом относительно бинарной операции если для любого элемента х из А выполняется условие x = x. (6
x = x. (6  )
) из А называется правым нейтральным относительно бинарной операции
из А называется правым нейтральным относительно бинарной операции  е
е  )
)


