1°. Если на множестве А существует нейтральный элементе, относительно бинарной операции  , то он регулярен относи-
, то он регулярен относи-
тельно  .
.
Доказательство. Из определения нейтрального элемента е следует выполнение условий:
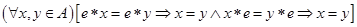 ,
,
которые равносильны условиям (11). Следовательно, е является регулярным относительно бинарной операции  .
.
ч.т.д.
2°. Если элементы r  и r
и r 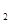 регулярны относительно ассоциативной бинарной операции
регулярны относительно ассоциативной бинарной операции 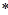 на А, то их композиция r
на А, то их композиция r 
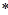 r
r 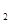 также является регулярным элементом относительно
также является регулярным элементом относительно  .
.
Доказательство. Пусть r  и r
и r 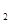 - регулярные элементы из А относительно бинарной операции
- регулярные элементы из А относительно бинарной операции  . Пусть х, у - элементы из А, удовлетворяющие условиям:
. Пусть х, у - элементы из А, удовлетворяющие условиям:
 , (12)
, (12)
 , (13)
, (13)
Поскольку бинарная операция  ассоциативная, то из (12) получаем
ассоциативная, то из (12) получаем
 ,
,
откуда в силу регулярности элемента r  имеем r
имеем r 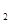
 х = r
х = r 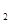
 у, далее, в силу регулярности элемента r
у, далее, в силу регулярности элемента r 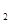 получаем х =у.
получаем х =у.
Итак,

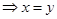 , то есть элемент r
, то есть элемент r 
 r
r 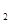 -
-  регулярен слева.
регулярен слева.
Аналогично доказывается, что элемент r 
 r
r 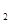 -регулярен справа:
-регулярен справа:
(13)  .
.
Следовательно, элемент r 
 r
r 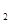 является регулярным на А относительно
является регулярным на А относительно  .
.
ч.т.д.
3°. Если элемент r регулярен относительно бинарной операции  на А, то он регулярен и относительно бинарной операции */A
на А, то он регулярен и относительно бинарной операции */A  , индуцированной этой операцией на каждом замкнутом относительно
, индуцированной этой операцией на каждом замкнутом относительно  подмножестве A
подмножестве A  , содержащем r (но элемент из A
, содержащем r (но элемент из A  может быть регулярным в A
может быть регулярным в A  , не будучи регулярным в А).
, не будучи регулярным в А).
п. 7. Симметричные элементы.
Когда речь идет о симметричных элементах алгебры (А;  ), то всегда имеется ввиду существование нейтрального элемента е.
), то всегда имеется ввиду существование нейтрального элемента е.
Пусть A = (A;  , e) - алгебра типа (2, 0).
, e) - алгебра типа (2, 0).
ОПРЕДЕЛЕНИЕ 17. Элемент s  (х) из А называется левымсимметричным к элементу х из А относительно бинарной операции
(х) из А называется левымсимметричным к элементу х из А относительно бинарной операции  , если выполняется условие:
, если выполняется условие:
s  (х)
(х)  x = e. (14)
x = e. (14)
ОПРЕДЕЛЕНИЕ 18. Элемент s  (x) из А называется правымсимметричным к элементу x из А относительно бинарной опера-ции
(x) из А называется правымсимметричным к элементу x из А относительно бинарной опера-ции  , если выполняется условие:
, если выполняется условие:
x  s
s  (x) = е.. (15)
(x) = е.. (15)
ОПРЕДЕЛЕНИЕ 19. Элемент s (x) из А называется симметричным к элементу х из А относительно бинарной операции  , если он является левым и правым симметричным к x, то есть выполняются условия:
, если он является левым и правым симметричным к x, то есть выполняются условия:
s (x)  x = x
x = x  s (x). 6)
s (x). 6)
Если для элемента х из А существует симметричный элемент s (x) относительно бинарной операции  , то х называется симметризуемым. Элементы х и s (x) называются взаимносимметричными.
, то х называется симметризуемым. Элементы х и s (x) называются взаимносимметричными.
При аддитивной записи бинарной операции  , симметричный к элементу х относительно сложения " + " элемент называется противоположным и обозначается через (-х). Элементы х и (- x) называются взаимно противоположными. Для них выполняются условия
, симметричный к элементу х относительно сложения " + " элемент называется противоположным и обозначается через (-х). Элементы х и (- x) называются взаимно противоположными. Для них выполняются условия
(- х) + х = х + (- x)= 0. (161)
При мультипликативной записи бинарной операции  , симметричный к элементу х относительно умножения “
, симметричный к элементу х относительно умножения “  “ элемент называется обратным и обозначается через х
“ элемент называется обратным и обозначается через х 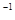 . Элементы х и х
. Элементы х и х 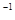 называются взаимно обратными. Для них выполняются условия:
называются взаимно обратными. Для них выполняются условия:
 . (16
. (16  )
)

 , то он регулярен относи-
, то он регулярен относи-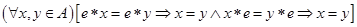 ,
, и r
и r 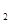 регулярны относительно ассоциативной бинарной операции
регулярны относительно ассоциативной бинарной операции 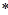 на А, то их композиция r
на А, то их композиция r  , (12)
, (12) , (13)
, (13) ,
,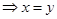 , то есть элемент r
, то есть элемент r  регулярен слева.
регулярен слева. .
. (х) из А называется левымсимметричным к элементу х из А относительно бинарной операции
(х) из А называется левымсимметричным к элементу х из А относительно бинарной операции  (x) из А называется правымсимметричным к элементу x из А относительно бинарной опера-ции
(x) из А называется правымсимметричным к элементу x из А относительно бинарной опера-ции  “ элемент называется обратным и обозначается через х
“ элемент называется обратным и обозначается через х 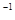 . Элементы х и х
. Элементы х и х  . (16
. (16  )
)


