44. Нейтральный элемент е относительно бинарной операции  на любом множестве, очевидно, является симметричным самому себе: s (е) = е.
на любом множестве, очевидно, является симметричным самому себе: s (е) = е.
45. На множестве натуральных чисел N относительно сложения (умножения) ни одно натуральное число n не имеет противоположного (обратного) натурального числа.
46. На множестве Z для любого целого числа z существует противоположное целое число - z относительно сложения.
47. В векторном пространстве  относительно сложения для любого вектора
относительно сложения для любого вектора  существует противоположный вектор -
существует противоположный вектор -  .
.
ОПРЕДЕЛЕНИЕ 1. Алгебра A =  типа (2) называется группоидом.
типа (2) называется группоидом.
ОПРЕДЕЛЕНИЕ 2. Подалгебра A  типа (2) группоида A
типа (2) группоида A  называется подгруппоидом.
называется подгруппоидом.
ОПРЕДЕЛЕНИЕ З. Бинарная операция  называется ассоциативной, если выполняется условие
называется ассоциативной, если выполняется условие
 .
.
ОПРЕДЕЛЕНИЕ 4. Алгебра A  типа (2) с ассоциатив-ной бинарной операцией
типа (2) с ассоциатив-ной бинарной операцией  называется полугруппой.
называется полугруппой.
ОПРЕДЕДЕНИЕ 5. Бинарная операция  на множества А называется коммутативной, если для любых элементов х, у из А выполняется условие
на множества А называется коммутативной, если для любых элементов х, у из А выполняется условие
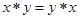 .
.
ОПРЕДЕЛЕНИЕ 6. Центральным элементом множества А относительно бинарной операции  называется каждый элемент с, перестановочный со всеми элементами х из А:
называется каждый элемент с, перестановочный со всеми элементами х из А:
 .
.
ОПРЕДЕЛЕНИЕ 7. Бинарная операция т называется двояко дистрибутивной или просто дистрибутивной относительно бинарной операции  , если выполняется условие:
, если выполняется условие:

 T
T 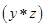
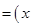 T
T  T
T  T
T  T
T  T
T  .
.
ОПРЕДЕЛЕНИЕ 8. Говорят, что бинарная операция  на множестве А является обратимой, если выполняется условие
на множестве А является обратимой, если выполняется условие
 .
.
ОПРЕДЕЛЕНИЕ 9. Элемент e  из А называется левым нейтральным элементом относительно бинарной операции если для любого элемента х из А выполняется условие
из А называется левым нейтральным элементом относительно бинарной операции если для любого элемента х из А выполняется условие
e 
 x = x.
x = x.
ОПРЕДЕЛЕНИЕ 10. Элемент е 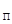 из А называется правым нейтральным относительно бинарной операции
из А называется правым нейтральным относительно бинарной операции  , если для любого элемента х из А выполняется условие
, если для любого элемента х из А выполняется условие
x  е
е  = x.
= x.
ОПРЕДЕЛЕНИЕ 11. Элемент е из А называется нейтральным относительно бинарной операции  , если он является левым и правым нейтральным, то есть для любого элемента х из А выполняются условия
, если он является левым и правым нейтральным, то есть для любого элемента х из А выполняются условия
e  x = х
x = х  е = х.
е = х.
ОПРЕДЕЛЕНИЕ 12. Алгебра A =(А;  , е) типа (2, 0) с ассоциативной бинарной операцией
, е) типа (2, 0) с ассоциативной бинарной операцией  называется моноидом.
называется моноидом.
ОПРЕДЕЛЕНИЕ 13. Элемент  называется поглощающим относительно этой операции, если для любого
называется поглощающим относительно этой операции, если для любого  выполняется равенства
выполняется равенства
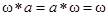 .
.
ОПРЕДЕЛЕНИЕ 14. Элемент r  из А называется регулярным слева относительно бинарной операции
из А называется регулярным слева относительно бинарной операции  , если выполняется условие:
, если выполняется условие:
 .
.
ОПРЕДЕЛЕНИЕ 15. Элемент r  из А называется регулярным справа относительно бинарной операции
из А называется регулярным справа относительно бинарной операции  , если выполняется условие:
, если выполняется условие:
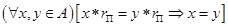 .
.
ОПРЕДЕЛЕНИЕ 16. Элемент r из А называется регулярным относительно бинарной операции  , если он регулярен слева и справа относительно
, если он регулярен слева и справа относительно  , то есть выполняются условия:
, то есть выполняются условия:
 .
.
ОПРЕДЕЛЕНИЕ 17. Элемент s  (х) из А называется левымсимметричным к элементу х из А относительно бинарной операции
(х) из А называется левымсимметричным к элементу х из А относительно бинарной операции  , если выполняется условие:
, если выполняется условие:
s  (х)
(х)  x = e.
x = e.
ОПРЕДЕЛЕНИЕ 18. Элемент s  (x) из А называется правымсимметричным к элементу x из А относительно бинарной опера-ции
(x) из А называется правымсимметричным к элементу x из А относительно бинарной опера-ции  , если выполняется условие:
, если выполняется условие:
x  s
s  (x) = е.
(x) = е.
ОПРЕДЕЛЕНИЕ 19. Элемент s (x) из А называется симметричным к элементу х из А относительно бинарной операции  , если он является левым и правым симметричным к x, то есть выполняются условия:
, если он является левым и правым симметричным к x, то есть выполняются условия:
s (x)  x = x
x = x  s (x).
s (x).

 на любом множестве, очевидно, является симметричным самому себе: s (е) = е.
на любом множестве, очевидно, является симметричным самому себе: s (е) = е. относительно сложения для любого вектора
относительно сложения для любого вектора  существует противоположный вектор -
существует противоположный вектор -  типа (2) называется группоидом.
типа (2) называется группоидом. типа (2) группоида A
типа (2) группоида A  называется подгруппоидом.
называется подгруппоидом. .
.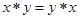 .
. .
.
 T
T 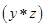
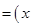 T
T  T
T  T
T  T
T  T
T  .
. .
. из А называется левым нейтральным элементом относительно бинарной операции если для любого элемента х из А выполняется условие
из А называется левым нейтральным элементом относительно бинарной операции если для любого элемента х из А выполняется условие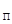 из А называется правым нейтральным относительно бинарной операции
из А называется правым нейтральным относительно бинарной операции  е
е  , е) типа (2, 0) с ассоциативной бинарной операцией
, е) типа (2, 0) с ассоциативной бинарной операцией  называется поглощающим относительно этой операции, если для любого
называется поглощающим относительно этой операции, если для любого  выполняется равенства
выполняется равенства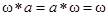 .
. .
.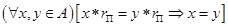 .
. .
. (x) из А называется правымсимметричным к элементу x из А относительно бинарной опера-ции
(x) из А называется правымсимметричным к элементу x из А относительно бинарной опера-ции 


