СВОЙСТВА СИММЕТРИЧНЫХ ЭЛЕМЕНТОВ
1°. Если бинарная операция Доказательство. Пусть
Отсюда по определению нейтрального элемента е и ассоциативно-сти бинарной операции
то есть
ч.т.д. 2°. Если элемент х из А имеет симметричный элемент s (x) относительно ассоциативной бинарной операции Доказательство. Свойство 2° является непосредственным следствием свойства 1°. 3 °. Если элементы х и у из А симметризуемы относительно ассоциативной бинарной операции Доказательство. Пусть s (y) и s (x) элементы, симметричные к: элементам х и у соответственно относительно ассоциативной бинарной операции
или то есть элемент s (y) Аналогично, элемент s (y)
Итак s (y) ч.т.д Свойство 3° кратко может быть записано в виде s (s Пример 43. Пусть (Z; +) - алгебра типа (2). Целое число 3 из Z является противоположным кцелому числу -3, а целое число -5 к целому числу 5. Тогда (-5)+3= -2 является противоположным целым числом к целому числу (-3) +5 = 2, так как ((-5)+ 3)+(З+(-5))=0 и (3+(-5)) + ((-5)+ 3) =0. 4 °. Элемент х из А, симметризуемый относительно ассоциативной бинарной операции Доказательство. Пусть х произвольный симметризуемый элемент из A, a s (x) -симметричный к х элемент. Предположим, что у и z из А - произвольные элементы, для которых выполнены условия: x y Из равенства (19) имеем s (x)
(s (x)
e
y = z Мы показали, что x Теперь из равенства (20) имеем (y
y
y
y = z то есть y Из условий (21), (22) получаем, что х - регулярный элемент относительно бинарной операции ч.т.д. Свойство 4 ° можно сформулировать еще так: Если элемент х из А симметризуем относительно ассоциативной бинарной операции Замечание. В некоторых учебных пособиях симметричный элемент к элементу х из А обозначается через х' или через х*.
|

 на А ассоциативная и элемент
на А ассоциативная и элемент  A -симметризуем, то существует единственный элемент, симметричный к х.
A -симметризуем, то существует единственный элемент, симметричный к х. (x) и
(x) и  (x)- элементы, симметричные к элементу х относительно ассоциативной бинарной операции
(x)- элементы, симметричные к элементу х относительно ассоциативной бинарной операции 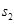 (x)
(x)  (x) =
(x) = 

 ,
, .
.
 y = z.
y = z.


