Пусть  - бинарная операция во множестве А.
- бинарная операция во множестве А.
ОПРЕДЕЛЕНИЕ 13. Элемент  называется поглощающим относительно этой операции, если для любого
называется поглощающим относительно этой операции, если для любого  выполняется равенства
выполняется равенства
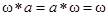 .
.
Таким образом 0 – поглощающий элемент относительно операции умножения.
Как и для нейтральных элементов, доказывается, что в А не может быть двух различных поглощающих элементов относительно операции  . В самом деле, если
. В самом деле, если  и
и  1 – поглощающие элементы, то
1 – поглощающие элементы, то 

 1 должно равняться и
1 должно равняться и  , и
, и  1, а потому
1, а потому  =
=  1.
1.
Если  - поглощающий элемент относительно операции
- поглощающий элемент относительно операции  , то любое выражение, содержащее лишь эту операцию, в которое входит
, то любое выражение, содержащее лишь эту операцию, в которое входит  , можно заменить на
, можно заменить на  .
.
Например, 
 .
.
п. 6. Регулярные элементы.
Пусть  - бинарная операция на множестве А.
- бинарная операция на множестве А.
ОПРЕДЕЛЕНИЕ 14. Элемент r  из А называется регулярным слева относительно бинарной операции
из А называется регулярным слева относительно бинарной операции  , если выполняется условие:
, если выполняется условие:
 . (9)
. (9)
По-другому, элемент r  из А регулярен слева, - если возможно " левое сокращение" на r
из А регулярен слева, - если возможно " левое сокращение" на r  .
.
ОПРЕДЕЛЕНИЕ 15. Элемент r 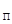 из А называется регулярным справа относительно бинарной операции
из А называется регулярным справа относительно бинарной операции  , если выполняется условие:
, если выполняется условие:
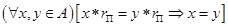 . 10)
. 10)
По-другому, элемент r 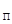 из А регулярен справа, - если возможно " правое сокращение" на r
из А регулярен справа, - если возможно " правое сокращение" на r 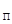 .
.
ОПРЕДЕЛЕНИЕ 16. Элемент r из А называется регулярным относительно бинарной операции  , если он регулярен слева и справа относительно
, если он регулярен слева и справа относительно  , то есть выполняются условия:
, то есть выполняются условия:
 .
.
Таким образом, в случае регулярности элемента r относительно бинарной операции  в равенствах типа r
в равенствах типа r  х = r
х = r  у и х
у и х  r=у
r=у  r возможно " сокращение" на r.
r возможно " сокращение" на r.

 - бинарная операция во множестве А.
- бинарная операция во множестве А. называется поглощающим относительно этой операции, если для любого
называется поглощающим относительно этой операции, если для любого  выполняется равенства
выполняется равенства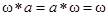 .
.
 из А называется регулярным слева относительно бинарной операции
из А называется регулярным слева относительно бинарной операции  . (9)
. (9)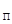 из А называется регулярным справа относительно бинарной операции
из А называется регулярным справа относительно бинарной операции 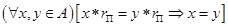 . 10)
. 10) .
.


