Пример 1.12. Даны матрицы А и В. Найти и сравнить произведения А В и В А.
Даны матрицы А и В. Найти и сравнить произведения А
Решение.
Видно, что
Очевидно, что для матриц выполняются следующее свойство: A если это умножение возможно. 3. Операция умножения матриц ассоциативна, т. е. (А 4. Операция умножения матриц дистрибутивна по отношению к алгебраическому сложению: А (А 5. Если произведение А
6. Если определено произведение А (А (A при условии, что определено произведение матриц А 7. Матрицу А можно умножать саму на себя только если она квадратная. Произведение А 8. Произведение двух матриц может дать нулевую матрицу, хотя ни одна из матриц-сомножителей не является нулевой (см. пример 1.12). Две матрицы называются эквивалентными или равносильными (но не равными), если одна из них может быть получена из другой следующими операциями, называемыми элементарными преобразованиями матриц: · перемена местами двух строк (столбцов); · умножение строки (столбца) на число, отличное от нуля; · прибавление (вычитание) к элементам одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число; · отбрасывание строки (столбца), целиком состоящей из нулей. При элементарных преобразованиях между эквивалентными матрицами ставится знак Известно, что в обычной алгебре можно вычислить многочлен, подставив в него вместо каждой переменной какое-то конкретное числовое значение. Аналогично можно вычислять матричные многочлены.
|

 В и В
В и В 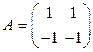 ;
; 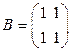 .
.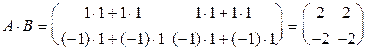 ;
;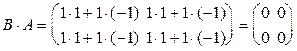 .
.
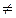
 , т.е.
, т.е.  . ►
. ►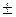 С) = А
С) = А  А
А 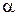 верно соотношение
верно соотношение (A
(A 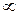 или ~. Зная основные операции над матрицами, можно производить вычисления матричных многочленов.
или ~. Зная основные операции над матрицами, можно производить вычисления матричных многочленов.


