Правило 2
Изобразим определитель дважды в виде 9 точек, каждая из которых означает соответствующий элемент. На левом рисунке проведем главную диагональ и два треугольника таким образом, чтобы одна сторона каждого треугольника была параллельна главной диагонали. Произведения элементов главной диагонали и произведения элементов, лежащих в вершинах обоих треугольников, берутся со знаком плюс. На правом рисунке проведем побочную диагональ и два треугольника со стороной, параллельной побочной диагонали. Соответствующие произведения входят в определитель со знаком минус. Выписываем сумму произведений матрицы, учитывая знаки. Замечание. Правило Сарруса может быть использовано только для вычисления определителя третьего порядка. · Вычисление определителя матрицы любого порядка разложение по строке или столбцу Запишем полученную формулу (1.1) определителя 3-го порядка и вынесем за скобку элементы первой строки:
Обозначим члены в скобках соответственно А 11, А 12 и А 13 и назовем их алгебраическими дополнениями элементов - соответственно а 11, а 12 и а 13. Тогда
Аналогичные равенства можно получить для элементов второй и третьей строки, а также для элементов любого столбца. Для i -й строки или для j -го столбца определителя n -го порядка такие равенства соответственно имеют вид:
Данная запись определителя называется разложением определителя по строке или столбцу.
Введем еще одно понятие. Минором Мij элемента aij определителя Например, для определителя третьего порядка
Для определителя n -го порядка можно строго доказать, что Aij = (–1) i + j Этот способ вычисления определителя является универсальным, т.к. позволяет вычислять определители любого порядка. ► Пример 1.18. Вычислить определитель матрицы Решение.
= –2 = –8 + 20 +11 = 23. ►
· Определитель треугольной матрицы Легко видеть, что если последовательно раскладывать определитель треугольной матрицы по элементам столбца, определитель представляет собой произведение элементов главной диагонали:
Свойства определителей: 1. Если какая-либо строка или какой-либо столбец определителя состоит только из нулей, то определитель равен нулю. Это сразу видно, если разложить определитель по нулевой строке или столбцу. Например:
2. При транспонировании матрицы ее определитель не изменяется: det A = det 3. Определитель произведения двух квадратных матриц равен произведению их определителей, то есть, если С = АВ, то det C = det A Отсюда следует, что, если даже 4. При перестановке любых двух строк или столбцов определитель не изменяется по абсолютной величине, но меняет знак на противоположный.
Например, перестановка первой и второй строки дает:
5. Определитель, содержащий 2 одинаковых строки или два одинаковых столбца, равен нулю. Действительно, если переставить эти две строки (столбца), то, с одной стороны, определитель должен поменять знак по свойству 4; с другой стороны - остаться неизменным, т. к. поменяли одинаковые строки (столбцы). Это возможно только когда определитель равен нулю.
Например:
Это свойство можно всегда проверить путем непосредственного вычисления определителя. 6. Общий множитель всех элементов какой-либо строки или столбца можно вынести за знак определителя. Например,
7. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения к элементам другой строки (столбца) равна нулю. Например, для определителя третьего порядка
= 8. Определитель не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число. Например:
|



 .
. = а 11 А 11+ а 12 А 12+ а 13 А 13.
= а 11 А 11+ а 12 А 12+ а 13 А 13. ;
; 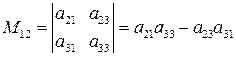 .
. Mij.
Mij.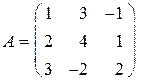 из предыдущего примера путем разложения его, например, по второй строке.
из предыдущего примера путем разложения его, например, по второй строке.

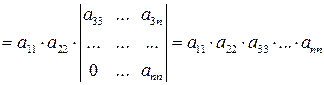 .
.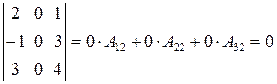 .
.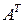 .
.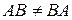 , то det(AB) = det(BA).
, то det(AB) = det(BA). .
.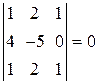 .
. .
. =
= .
. .
.


