Пример 1.15
В перестановке1 2 3 4 5 нет инверсий; В перестановке 1 2 4 3 5 - одна инверсия, образуемая парой чисел 4 и 3; В перестановке 4 3 5 1 2 - семь инверсий: 4 и 3; 4 и 1; 4 и 2; 3 и 1; 3 и 2; 5 и 1; 5 и 2. ►
Перестановка первых n натуральных чисел называется четной, если в ней четное число инверсий, и нечетной, если в ней нечетное число инверсий. Перейдем теперь непосредственно к понятию определителя матрицы n -го порядка (далее определитель). Рассмотрим квадратную матрицу А порядка n.
Выберем из матрицы А по одному элементу из каждой строки и каждого столбца. Технически это можно сделать, например, так. Возьмем какой-либо элемент из первой строки и вычеркнем тот столбец, из которого взяли элемент. Элемент второй строки берем из какого-либо невычеркнутого столбца и затем вычеркиваем этот столбец и т.д. Когда дойдем до последней n -й строки, останется один невычеркнутый столбец, из которого выбирается элемент матрицы, принадлежащий последней строке. Составим произведение взятых элементов, причем расположим элементы в произведении так, чтобы первые индексы располагались в порядке возрастания:
где вторые индексы элементов матрицы j 1, j 2 … jn — номера столбцов матрицы, причем все разные. Эти номера образуют перестановку натуральных чисел от одного до n. Очевидно, что всего таких возможных произведений ровно столько, сколько перестановок чисел от одного до n. Иначе говоря, таких произведений ровно n!, в каждом из которых n элементов. Рассмотрим каждую из таких перестановок и, если она нечетная, умножим произведение с такой перестановкой вторых индексов на (–1). Затем просуммируем все полученные таким образом n! членов.
Полученное число называется определителем (или детерминантом) матрицы А, или просто определителем n -го порядка.
Определитель обозначается det А или
Обозначение det А обычно используется тогда, когда рассматривается несколько матриц. Следует помнить, что хотя определитель записан в форме матрицы, он представляет собой одно число, которое вычисляется по указанному правилу. Заметим, что определитель матрицы первого порядка, состоящей из одного элемента, есть сам этот элемент. · Вычисление определителей второго и третьего порядка Запишем определитель второго порядка в общем матричном виде:
Число перестановок в определителе 2-го порядка равно 2! = 2, а каждая перестановка содержит 2 сомножителя. Возможны всего две перестановки вторых индексов: - перестановка 1 2 — ноль инверсий, т.е. перестановка четная; - перестановка 2 1 — одна инверсия, т.е. перестановка нечетная. Поэтому перед произведением а 12 а 21 нужно поставить знак минус. Запишем:
Таким образом, определитель второго порядка равен разности произведений элементов главной и побочной диагоналей.
|

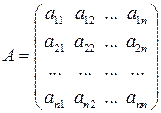 .
.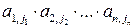 ,
, , но чаще всего определитель записывается также как и матрица, но не в круглых скобках, а в одиночных прямых линиях:
, но чаще всего определитель записывается также как и матрица, но не в круглых скобках, а в одиночных прямых линиях: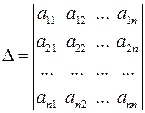 .
.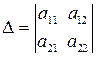 .
.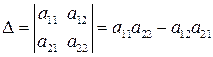 .
.


