Лекция 5. Ранг матрицыВ любой матрице Очевидно, что порядок k этих матриц будет удовлетворять неравенству k Определители таких матриц называются минорами k -го порядка матрицы А. Например, из матрицы Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы обозначается r(A), rang A, rank A.
Следствия определения ранга матрицы: 1) ранг матрицы 2) если r(A) = 0, то A – нулевая матрица; 3) ранг невырожденной квадратной матрицы n -го порядка равен n, а ранг вырожденной квадратной матрицы n -го порядка меньше n; 4) ранг матрицы 5) r(A + B) 7) r(AB)
|
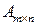вычеркиванием каких-либо строк или столбцов можно выделить квадратные матрицы k -го порядка.
min (m, n).
можно таким образом получить миноры 4-го, 3-го, 2-го и 1-го порядков. При этом минорами 1-го порядка называются отдельные элементы матрицы.
r(A) + r(B); 6) r(A + B) 
r(A) - r(B) 
;
