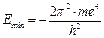Взаимодействия в атомах
Энергия притяжения электронов к ядру, а также энергия движения электронов, стремящаяся оторвать электрон от атома, уравновешены, и атом сохраняет устойчивое состояние. Только воздействие внешней среды способно вывести атом из этого состояния. В роли внешней среды выступают микрочастицы вещества (атомы, молекулы, электроны) и поля (фотоны). Рассмотрим атом водорода. По законам классической механики и электродинамики атом водорода – неустойчивая система. По законам квантовой механики, это устойчивая система, и сближение электрона с ядром не должно привести к его «падению» на ядро. В 1927 г. В. Гейзенберг сформулировал действующий в квантовой механике принцип неопределенности: объект микромира невозможно одновременно с наперед заданной точностью характеризовать координатой и импульсом. Если неопределенность в определении координаты х составляет D х, а неопределенность в определении импульса mu составляет D(mu), то неопределенности этих величин удовлетворяют условию (1.1)
где m – масса; u – скорость микрочастицы, движущейся вдоль координаты х; h – постоянная Планка.
Уравнение (1.1) получило название соотношения неопределенности Гейзенберга. Потенциальная энергия (Е) атома водорода складывается из кинетической энергии электрона (U): U = и энергии притяжения электрона ядром (V). Заряды ядра (в данном случае протона) и электрона равны по величине и противоположны по знаку (заряд е):
Е = U + V = где u - скорость движения электрона массой m; r – радиус орбитали. Состояние электрона с точно установленными значениями координаты r и импульса mu означало бы нарушение соотношения неопределенности Гейзенберга. Допустим, что неопределенность в определении координаты имеет порядок самой координаты (D r» r), а неопределенность в определении импульса имеет порядок самого импульса (D mu» mu). Согласно соотношению неопределенности получим: r × mu = Подставляя значение u из уравнения (1.3) в выражение потенциальной энергии (1.2), получим: Е = Устойчивому состоянию атома соответствует минимум потенциальной энергии
Отсюда Полученное значение r min совпадает с радиусом первой боровской орбиты атома водорода. Подставив r min из уравнения (1.5) в уравнение (1.4), найдем энергию основного состояния атома водорода:
Эта величина соответствует минимальной энергии атома водорода (рис. 4).
|

 , (1.1)
, (1.1)

 , (1.2)
, (1.2) (1.3)
(1.3)
 . Продифференцировав выражение (1.4) по r и приравняв
. Продифференцировав выражение (1.4) по r и приравняв  , получим:
, получим: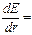 -
-  +
+  = 0.
= 0. (1.5)
(1.5)