К задаче 1
1. Находим расчётные значения нагрузок, по условию задачи F, M – нагрузки постоянные. F= M= Где Где 2. Определяем опорные реакции и производим проверку их правильности. 3. Обозначаем характерные точки (сечения) балки. Ими являются концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки. 4. Строим эпюру поперечных сил. Для этого определяем значения поперечных сил в характерных точках. Поперечная сила в сечении равна алгебраической сумме проекции всех сил, расположенных только слева или только справа от рассматриваемого сечения на ось, перпендикулярно к оси балки. Сила, приложенная слева от рассматриваемого сечения и направленная вверх, принимается со знаком «+», а сила, направленная вниз со знаком «-», а для правой части балки – наоборот. В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: на бесконечном малом расстоянии левее рассматриваемой точки и правее ее. Поперечная сила в этих сечениях обозначается соответственно 5. Строим эпюру изгибающих моментов М. Для этого определяем изгибающие моменты в характерных точках (сечениях). Изгибающий момент в рассматриваемом сечении равен алгебраической сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения, относительно центра тяжести этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то момент принимается со знаком «+», а если против – со знаком «-», а для правой части – наоборот. В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: на бесконечно малом расстоянии левее рассматриваемой точки и правее ее. Изгибающие моменты в этих точках обозначаются соответственно В точках приложения сил определяется одно значение изгибающего момента. Если на участке балки нет распределенной нагрузки, то под этим участком два соседних значения моментов соединяются прямой линии. Если на участке балки приложена распределенная нагрузка, то под этим участком значение изгибающих моментов для двух соседних точек соединяются квадратичной параболой. Парабола направлена выпуклостью в сторону действия нагрузки (при действии нагрузки сверху парабола обращена выпуклостью вниз). При этом, если на эпюре на рассматриваемом участке наклонная прямая не пересекает нулевую линию, то на эпюре М парабола может быть построена по двум точкам, так как все значения изгибающих моментов в промежуточных точках, так как все значения изгибающих моментов в промежуточных точках находятся между значениями в характерных сечениях. Если на эпюре Q наклонная прямая пересекает нулевую линию, то в этом сечении изгибающий момент имеет экспериментальное значение (максимальное или минимальное). Существует несколько способов проверки правильности построения эпюр. Наиболее простой способ заключается в том, что значения Q и M взятые отдельно по левым и правым силам должны быть равны между собой. 6. Подбирают сечение стальной двутавровой балки в следующем порядке: а) определяют требуемый осевой момент сопротивления балки
Где /
7. Проверяют прочность принятой двутавровой балки по нормальным напряжениям. Такую проверку выполняют для сечения с наибольшим изгибающим моментом.
Где 8. Строят эпюру нормальных напряжений 9. Проверяют прочность принятой двутавровой балки по касательным напряжениям. Наибольшее касательное напряжение будут в том сечении балки, где действует наибольшая поперечная сила (по численному значению), а по высоте сечения – на уровне нейтрального слоя. Для определения этих напряжений действительное сечение двутавровой балки принимают упрощённым. Полки и стенка принимаются прямоугольными, полка размером b и t, стенка размером Sи (h-2t), S – толщина стенки, в некоторых справочниках обозначается буквой d. Наибольшее касательное напряжение на уровне нейтрального слоя определяют по формуле Журавского:
где 10. Строят эпюру касательных напряжений. Касательные напряжения измеряются по высоте поперечного сечения балки по криволинейному закону. Эпюру касательных напряжений строят для стенки двутавра по значениям, найденным в трёх точках сечения: на уровне нейтральной оси и на уровне сопряжения стенки с полками. Пи этом статический момент
К задаче 2
|



 – коэффициент надёжности по нагрузке для постоянной нагрузки.
– коэффициент надёжности по нагрузке для постоянной нагрузки. ,
,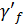 – коэффициент надёжности по нагрузке для временной нагрузки,
– коэффициент надёжности по нагрузке для временной нагрузки,  - временная нагрузка.
- временная нагрузка. и
и  Найденные значения поперечных сил в характерных точках отложим в некотором масштабе от нулевой линии параллельной оси балки. Если на участке балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяется прямой линией, параллельной оси балки, если на участке балки приложена, распределенная нагрузка, то под этим участком значения поперечных сил соединяем прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.
Найденные значения поперечных сил в характерных точках отложим в некотором масштабе от нулевой линии параллельной оси балки. Если на участке балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяется прямой линией, параллельной оси балки, если на участке балки приложена, распределенная нагрузка, то под этим участком значения поперечных сил соединяем прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию. и
и  Полученные значения откладываем в некотором масштабе от нулевой линии. Эпюра изгибающих моментов строится по растянутым волокнам, то – есть если растягиваются нижние волокна балки, то значения изгибающих моментов откладываются вниз от нулевой линии, если растягиваются верхние волокна – вверх от нулевой линии. При положительных изгибающих моментах растягиваются нижние волокна, при отрицательных – верхние.
Полученные значения откладываем в некотором масштабе от нулевой линии. Эпюра изгибающих моментов строится по растянутым волокнам, то – есть если растягиваются нижние волокна балки, то значения изгибающих моментов откладываются вниз от нулевой линии, если растягиваются верхние волокна – вверх от нулевой линии. При положительных изгибающих моментах растягиваются нижние волокна, при отрицательных – верхние.
 - наибольший по численному значению изгибающий момент;
- наибольший по численному значению изгибающий момент;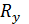 - расчётное сопротивление материала по пределу текучести;
- расчётное сопротивление материала по пределу текучести;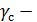 коэффициент условия работы.
коэффициент условия работы.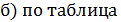 ГОСТов (приложение 1) подбираем номер двутавровой стальной балки, которая должна иметь момент сопротивления
ГОСТов (приложение 1) подбираем номер двутавровой стальной балки, которая должна иметь момент сопротивления 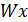 наиболее близкий по значению к требуемому моменту сопротивления
наиболее близкий по значению к требуемому моменту сопротивления 

 - момент сопротивления принятого сечения.
- момент сопротивления принятого сечения. Для этого вычеркивают крупно поперечное сечение балки и проводят на отдельном рисунке нулевую линию, перпендикулярно нейтральной оси. Затем на уровне крайних точек сечения (верхней и нижней) откладывают найденные значения
Для этого вычеркивают крупно поперечное сечение балки и проводят на отдельном рисунке нулевую линию, перпендикулярно нейтральной оси. Затем на уровне крайних точек сечения (верхней и нижней) откладывают найденные значения  и соединяют эти значения прямой линией. Значение
и соединяют эти значения прямой линией. Значение  откладывают правее нулевой линии,
откладывают правее нулевой линии,  - левее. Следует иметь в виду, что при положительном значении
- левее. Следует иметь в виду, что при положительном значении  наибольшее напряжение
наибольшее напряжение  будут в крайних нижних точках, при отрицательном значении
будут в крайних нижних точках, при отрицательном значении  -
-  будут в верхних точках сечения.
будут в верхних точках сечения.
 – статический момент той части сечения, которая расположена выше или ниже нейтральной оси. Для определения
– статический момент той части сечения, которая расположена выше или ниже нейтральной оси. Для определения  значение
значение 



