СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Решению задач данной контрольной работы (за исключением задачи 1) должно предшествовать изучение основ расчета по предельным состояниям. В расчете по предельному состоянию единый коэффициент запаса заменен системой из нескольких коэффициентов, раздельно учитывающих условия возведения и работы конструкций, изменчивость нагрузок, изменчивость прочностных характеристик материалов. Рассмотрим некоторые вопросы, связанные с расчетом по несущей способности. Основными параметрами сопротивления материалов силовым воздействиям являются нормативные сопротивления Отношение R / = Основными характеристиками нагрузок (воздействий) являются их нормативные величины ( В расчетах по несущей способности принимают расчетные нагрузки, получаемые путем умножения их нормативных значений на коэффициенты перегрузки ( Особенности действительной работы конструкций, имеющие систематический характер, но не отражаемые в расчетах прямым путем, учитываются в необходимых случаях коэффициентами условий работы. Коэффициент условий работы учитывает влияние температуры, влажности и агрессивности среды, длительности воздействия, его многократной повторяемости и т. д.; приближенности расчетных схем и принятых в расчёте предпосылок; перераспределения силовых факторов и видов нагружения. Более полно расчет по предельным состояниям изучается в таких специальных предметах, как «Строительные конструкции» и др. К ЗАДАЧЕ 4 Цель задачи — научить подбирать сечение элементов конструкции, работающей на осевое растяжение или сжатие. Условие задачи. Для стержней 1 и 2 фермы, рассмотренной в первой задаче первой контрольной работы, подобрать сечение из равнополочной уголковой стали, принимая Решение. Воспользуемся формулой, характеризующей работу конструкции при осевом растяжении (сжатии): N откуда определяем требуемую площадь
где N — расчетная сила, возникающая в рассматриваемом элементе. Для простоты расчетов примем заданную нагрузку за расчетную, и силы, найденные в задаче 1 контрольной работы 1, также будут расчетными:
Определяем требуемую площадь сечения для стержня 2
По найденным К ЗАДАЧЕ 5 Цель задачи — проверка степени усвоения понятия геометрических характеристик поперечного сечения при изгибе и кручении. Перед решением задачи следует повторить из теоретической механики учебный материал, касающийся определения центра тяжести сечений, составленных из простейших геометрических фигур, и сечений из прокатных профилей, определение статического момента площади сечения относительно произвольных осей координат. Обращается внимание учащегося на различие геометрических характеристик поперечного сечения бруса при его растяжении (сжатии) и при изгибе или кручении. При растяжении (сжатии) площадь поперечного сечения бруса, являющаяся его геометрической характеристикой, полностью определяет сопротивление элемента растяжению (сжатию). Объясняется это тем, что при осевом растяжении или сжатии нормальные напряжения в сечениях центрально растянутого (сжатого) бруса распределяются равномерно. При неравномерном распределении напряжений по сечению бруса или балки, например при изгибе, на их деформирование влияет не площадь поперечного сечения, а его форма и, кроме того, положение осей поперечного сечения к направлению действия внешних сил. Поэтому при расчете балок на изгиб в сопротивлении материалов возникает необходимость принять геометрические характеристики поперечного сечения элемента называемые осевыми моментами инерции Порядок решения задач на определение момента инерции сечения плоских фигур следующий: 1.Разбить данную фигуру на простые составные части (прямоугольники, круги, треугольники и т. д.). Если в состав фигуры входит стандартный прокатный профиль, то последний не разбивается на части; положение его центра тяжести и площадь определяются по сортаментным таблицам (см. приложения). Простыми элементами в этом случае будут: двутавр, швеллер, уголки, полоса. Если фигура имеет отверстие, то площади и моменты инерции этих отверстий считают отрицательными. 2.Определить центр тяжести всей фигуры. 3.Через найденный центр тяжести сечения провести главные центральные оси. Для фигур, имеющих оси симметрии, главные оси совпадают с осями симметрии.
5.Определить расстояние между собственными главными осями каждой простой фигуры и главными центральными осями сечения в целом. Нанести эти расстояния а на чертеж. 6.Определить моменты инерции составных частей относительно собственных осей инерции 7.Определить моменты инерции сечения относительно главных центральных осей, используя формулу перехода на центральные оси: I= I
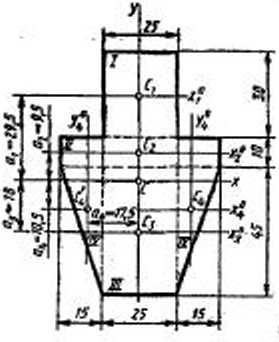
Решение. а) На изображение заданного сечения, вычерченного в. выбранном масштабе (рис. 15), наносим главные центральные оси. Ось у совмещаем с осью симметрии, ось х проводим перпендикулярно ей через центр тяжести С всей фигуры. Через центры тяжести Используя координаты центров тяжести частей фигуры, найденные при определении положения центра тяжести всей фигуры (см. рис. 9), определим расстояния между главной центральной осью х и каждой из осей
Используя формулу перехода на параллельные оси, определяем
Числовые значения площадей отдельных фигур берем также из контрольной работы 1:
Момент инерции относительно главной центральной оси х определим, суммируя моменты инерции составных частей фигуры:
Момент инерции относительно главной центральной оси у определяем следующим образом. Поскольку у фигур I, II, III собственные центральные оси совпадают с главной центральной осью инерции, расстояние между осями равно нулю. Следовательно, главный центральный момент инерции каждой из этих фигур равен собственному моменту инерции:
Для четвертой фигуры расстояние между вертикальными осями
Суммируя, получаем б) В составном сечении (рис. 16) через найденный центр тяжести С проводим главные центральные оси инерции х и у. Ось х совмещена с осью симметрии сечения. Проводим собственные центральные оси инерции Определим расстояния между собственными и главными центральными осями инерции, используя абсциссы центров тяжести частей сечения, найденные при определении положения центра тяжести всего сечения (см. рис. 10):
Выпишем из таблиц сортамента (см. приложения 1-4) моменты инерции
Для уголка значения моментов инерции Определяем главный центральный момент инерции составного сечения относительно оси х:
Определяем главный центральный момент инерции составного сечения относительно оси у:
Задачи для контрольной работы 1 Задача 1. Определить усилия в стержнях 1, 2, 3, 4 фермы аналитическим способом. Графическим способом только в стержнях 1, 2.Данные для задачи своего варианта взять из таблицы 1 и схемы на рис. 11. Задача 2. Определить опорные реакции балок. Данные для задачи взять из таблицы 2 и схемы на рис. 12 согласно своему варианту. Задача 3. Определить положение центра тяжести плоской фигуры геометрической формы и сечения, составленного из прокатных профилей. Данные для задачи своего варианта взять из таблицы 3 и схемы на рис. 13. Задача 4. Подобрать сечение стержней 1 и 2 фермы из уголковой стали, приняв найденные усилия в стержнях за расчетные. Расчетное сопротивления стали Задача 5. Найти главные центральные моменты инерции сечения: а) геометрической формы; б) составленного из стандартных профилей проката. Данная задача является продолжением задачи 3 согласно своему варианту
К задаче 1
К задаче 2
К задаче 3
К задаче 2
|

 . За нормативное сопротивление пластичного материала принимают предел текучести, для хрупкого — предел прочности (их наименьшие значения по ГОСТу). Возможные отклонения сопротивлений материалов в неблагоприятную сторону от нормативных значений учитываются коэффициентом надежности по материалу. Значения его в расчетах по несущей способности принимаются не менее 1.1.
. За нормативное сопротивление пластичного материала принимают предел текучести, для хрупкого — предел прочности (их наименьшие значения по ГОСТу). Возможные отклонения сопротивлений материалов в неблагоприятную сторону от нормативных значений учитываются коэффициентом надежности по материалу. Значения его в расчетах по несущей способности принимаются не менее 1.1. называется расчетным сопротивлением. Оно и принимается при расчете конструкций.
называется расчетным сопротивлением. Оно и принимается при расчете конструкций.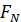 ;
;  и др.). Возможные отклонения нагрузок в неблагоприятную (большую ' или меньшую) сторону от их нормативных значений вследствие изменчивости нагрузок или отступлений от условий нормальной эксплуатации учитываются коэффициентом перегрузки устанавливаемыми с учетом назначения, зданий и сооружений и условий их эксплуатации.
и др.). Возможные отклонения нагрузок в неблагоприятную (большую ' или меньшую) сторону от их нормативных значений вследствие изменчивости нагрузок или отступлений от условий нормальной эксплуатации учитываются коэффициентом перегрузки устанавливаемыми с учетом назначения, зданий и сооружений и условий их эксплуатации. = F; q=
= F; q=  M=
M= 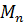 )
)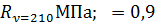
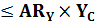

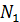 =16 кН = 0, 016 МН,
=16 кН = 0, 016 МН, 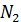 =19, 8 кН = 0, 0198 МН. Определение расчетных нагрузок рассмотрено в последующих задачах. Определяем требуемую площадь сечения для стержня 1.
=19, 8 кН = 0, 0198 МН. Определение расчетных нагрузок рассмотрено в последующих задачах. Определяем требуемую площадь сечения для стержня 1.

 и
и  в графе «Площадь сечения» таблицы сортамента (см.приложение 1) подбираем наиболее близкое значение площади, а следовательно, и номер профиля. Принимаем для стержня 1 равнополочный уголок 20
в графе «Площадь сечения» таблицы сортамента (см.приложение 1) подбираем наиболее близкое значение площади, а следовательно, и номер профиля. Принимаем для стержня 1 равнополочный уголок 20 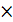 20
20  для стержня 2- точно такой же.
для стержня 2- точно такой же. или
или  .
. 4.Через центры тяжести простых фигур провести собственные центральные оси инерции.
4.Через центры тяжести простых фигур провести собственные центральные оси инерции. +
+ 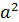 А.
А.
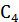 простых фигур проводим собственные центральные оси инерции. Обозначим их соответственно
простых фигур проводим собственные центральные оси инерции. Обозначим их соответственно  ,
, 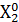 ,
,  Собственные центральные оси,
Собственные центральные оси,  ,
,  ,
,  совпадают с главной центральной осью.
совпадают с главной центральной осью. .
. =
=  -
- 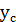 =70- 40, 5 = 29, 5 см;
=70- 40, 5 = 29, 5 см; =
=  -
-  = 50 - 40, 5 = 9, 5 см;
= 50 - 40, 5 = 9, 5 см; =
=  = 40, 5 - 22, 5 = 18 см;
= 40, 5 - 22, 5 = 18 см; =
=  = 40, 5 - 30 == 10, 5 см;
= 40, 5 - 30 == 10, 5 см; =
=  +
+  =
=  +
+  +29,
+29,  750=708937, 5 см.
750=708937, 5 см. =
= 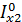 +
+  =
=  +9,
+9,  .
. =
=  +
+  =
=  +
+  .
. =2(
=2( +
+ 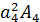 =2(
=2( +
+  +10,
+10,  =
=  +
+  +
+  =
=  =
=  =
=  =39.062
=39.062  =
=  =
=  =138, 646
=138, 646  =
= 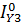 =
=  =
=  =58, 594
=58, 594 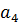 = 17, 5 см. (рис. 15):
= 17, 5 см. (рис. 15): =2(
=2( +
+  +17,
+17, 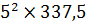 )=230156
)=230156  =466 458
=466 458  каждой из составных частей.
каждой из составных частей.


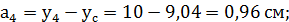
 h шв. №20+
h шв. №20+  h листа = 10, 6 см;
h листа = 10, 6 см;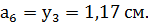
 прокатных профилей относительно собственных осей и их площади: двутавр № 20
прокатных профилей относительно собственных осей и их площади: двутавр № 20  ;
;  = 115
= 115  = 26, 8
= 26, 8 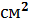 ; швеллер №20
; швеллер №20  2 = 1520
2 = 1520  = 113
= 113  = 23, 4
= 23, 4 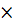 50
50 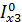 = 14, 8
= 14, 8 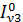 = 49
= 49  = 7, 55
= 7, 55 
 I
I  ;
;  =24
=24 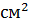 .
.
 +2(
+2( 
 = 1, 0. Данные для своего варианта взять из задачи 1.
= 1, 0. Данные для своего варианта взять из задачи 1.









 г
г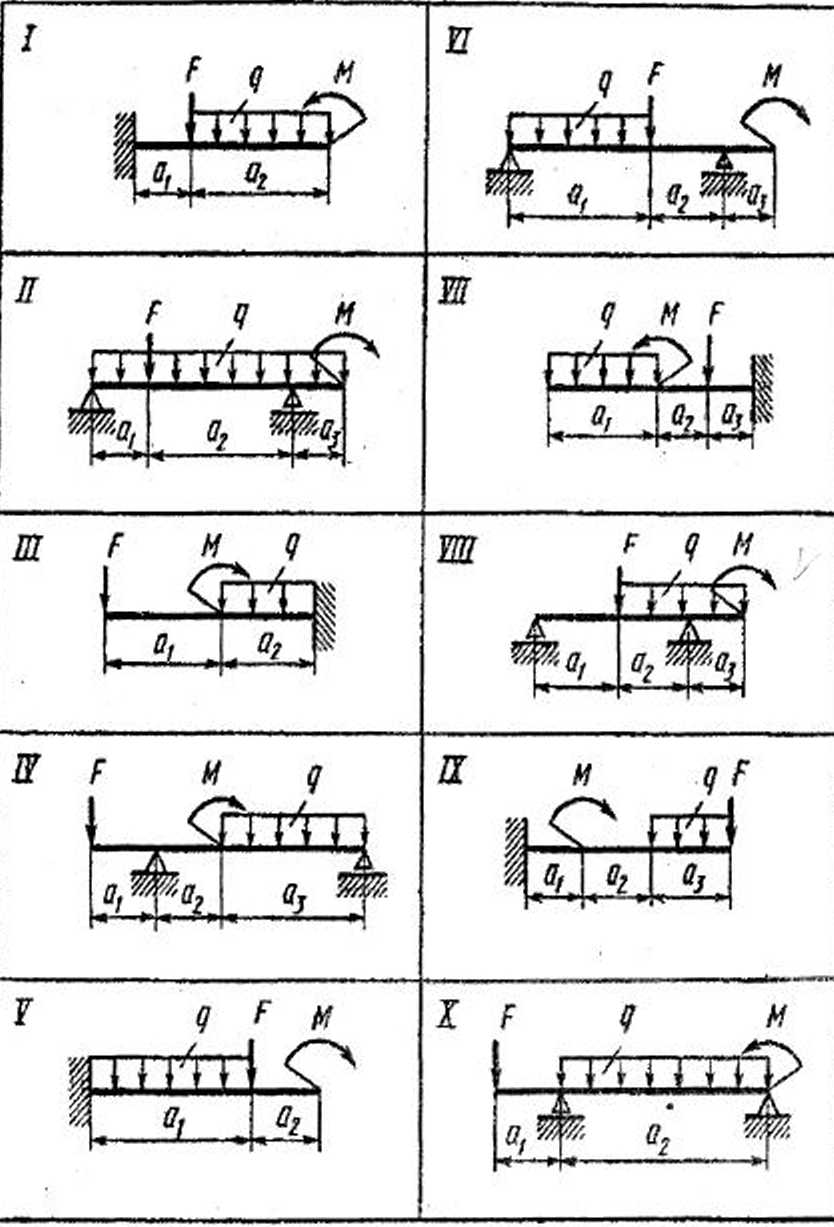



 К задаче 1
К задаче 1







 К задаче 3
К задаче 3







