ПРОГРАММА
Тема 3.1. Основные положения. Задачи статики сооружений, ее связь с теоретической механикой, сопротивлением материалов и смежными специальными предметами. Основные рабочие гипотезы. Классификация сооружений и их расчетных схем. Краткий обзор развития статики сооружений. Тема 3.2Кинематический анализ зачетных схем сооружений. Геометрически неизменяемые и изменяемые системы. Степень свободы. Необходимое условие геометрической неизменяемости. Анализ геометрической структуры сооружений. Мгновенно изменяемые системы. Понятие о статически определимых и неопределимых системах. Тема. 3.3. Статически определимые плоские фермы. Общие сведения о фермах. Развитие ферм поперечного сечения балок и предпосылки перехода от балки к ферме. Классификация ферм: по назначению, направлению опорных реакций, очертанию поясов, системе решетки. Образование простейших ферм. Условия геометрической неизменяемости и статической определимости ферм. Анализ геометрической структуры ферм. Аналитическое определение опорных реакций. Аналитическое определение сил в стержнях ферм методом вырезания узлов и сквозных сечений (способы моментных точек и проекций). Графическое определение сил в стержнях ферм путем построения диаграммы Максвелла — Кремоны. Тема 3.4. Статически определимые (составные) балки. Основные сведения о много пролетных статически определимых (шарнирных) балках. Условия статической определимости и геометрической неизменяемости. Анализ геометрической структуры. Типы шарнирных балок. Схемы взаимодействия (этажные схемы) элементов, составляющих шарнирные балки. Построение эпюр поперечных сил и изгибающих моментов. Понятие о наивыгоднейшем расположении шарниров в балке (равномоментные балки). Тема 3.5. Статически определимые плоские рамы. Общие сведения о рамных конструкциях. Анализ статической неопределимости рамных систем. Построение эпюр поперечных сил, изгибающих моментов и продольных сил. Проверка правильности построения эпюр по условиям равновесия жестких узлов и отсекаемых частей рамы (статическая проверка). | Тема 3.6. Трехшарнирные системы. Криволинейная балка. Общие сведения об арках. Типы арок и их элементы. Аналитический способ расчета трехшарнирных арок. Определение опорных реакций. Определение поперечной силы, изгибающего момента и продольной силы в произвольном сечении арки. Построение эпюр поперечных сил, изгибающих моментов и продольных сил. Понятие о расчете арки с затяжкой. Выбор рационального очертания оси арки. Тема 3.7. Определение перемещений в статически определимых плоских системах. Общий принцип обозначения перемещений. Формула Мора для элемента сооружений, испытывающего совместную деформацию изгиба с растяжением (сжатием). Примеры определения перемещений в статически определимых плоских системах методом Мора с применением правила Верещагина. Тема 3.8. Основы расчета статически неопределимых систем методом сил, Общие понятия о статически неопределимых системах. Степень статической неопределимости. Основная система. Канонические уравнения метода сил. Принцип и порядок расчета статически неопределимых систем методом сил. Применение метода сил к расчету статически неопределимых однопролетных балок и простейших рам с одним или двумя лишними неизвестными. Выбор рациональной основной системы. Проверка правильности эпюр. СПИСОК ЛИТЕРАТУРЫ Портаев Л. П., Петраков П.А., Портаев В.Л. Техническая механика, М., 1987. Мухин Н. В., Шишман Б. А., Першин А. Н. Статика сооружений. М., 1980. Мухин И. В. Статика сооружений в примерах. М., 1979. Улитин Н. С, Першин А. Н., Лауенбург Л. В. Сборник задач по технической механике. М., 1978.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ К теме 3.1. 1. Каковы задачи статики сооружений? 2. Что такое расчетная схема сооружения? От чего зависит ее выбор? 3. Как классифицируются сооружения? Каковы основные особенности расчетных схем каждого вида сооружений? 4. Как классифицируются опоры? 5. Какие существуют виды нагрузок? 6. Как определяют расчетные нагрузки? 7. Укажите роль отечественных ученых в развитии строительной механики. К теме 3.2. 1. Какие системы называют геометрически изменяемыми и мгновенно изменяемыми? 2. Каковы основные признаки геометрически неизменяемых систем? 3. Как выявляется геометрическая неизменяемость систем? 4. Каковы признаки мгновенной изменяемости систем? 5. Приведите примеры геометрической неизменяемой, изменяемой и мгновенно изменяемой систем. Произведите анализ их геометрической структуры.6. Можно ли применять в строительстве изменяемые, мгновенно изменяемые и почти мгновенно изменяемые системы? Если нельзя, то почему? 7. Каково различие между статически определимыми и неопределимыми системами? 8. Какие связи называют необходимыми и какие лишними? К теме 3.3. 1. Из каких элементов состоят фермы? 2. Каковы преимущества фермы по сравнению с балкой? 3. Приведите пример геометрически неизменяемой статически определимой фермы. Образуйте из нее геометрически изменяемую систему, оставив то же количество стержней. 4. Какого рода деформации испытывают стержни шарнирной фермы при узловой и внеузловой передаче нагрузки? 5. В чем сущность определения сил в стержнях ферм способами вырезания узлов, моментных точек и проекций? 6. Каковы принцип и порядок построения диаграммы Максвелла — Кремоны? 7. Как с помощью диаграммы Максвелла — Кремоны определить значение и знак силы в стержне? К теме 3.4. 1. Чем отличаются многопролетные определимые балки от неразрезных? 2. Какие требования предъявляются к количеству и размещению промежуточных шарниров? 3. Какие существуют основные типы шарнирных балок и из каких элементов они состоят? 4. Приведите возможные варианты размещения промежуточных шарниров для получения шарнирных статически определимых балок из неразрезной пяти пролетной балки с шарнирными опорами и из неразрезной пятипролетной балки с одним защемленным концом. Составьте схемы взаимодействия элементов шарнирных балок. 5. Каковы порядок расчета и последовательность монтажа элементов шарнирных балок? 6. Охарактеризуйте методы расчета шарнирных балок с составлением и без составления схемы взаимодействия элементов. Каковы достоинства и недостатки каждого из методов? 7. В чем достоинства равномоментных шарнирных балок? К теме 3.5. 1. Назовите особенности рамных конструкций. 2. Каково различие в определении опорных реакций статически определимых рам, не имеющих промежуточных шарниров, и рам с промежуточными шарнирами? 3. Как определяют знаки поперечных сил, изгибающих моментов и продольных сил при расчете рам? 4. Как строятся эпюры К теме 3.6. 1. В чем отличие распорной системы от безраспорной? 2. Каково назначение затяжки (в случае устройства арки с затяжкой)? 3. Как определяется сила в затяжке? 4. По каким правилам определяют поперечные силы, изгибающие моменты и продольные силы в сечениях арки? 5. Почему для построения эпюр К теме 3.7. 1.Какими буквами принято обозначать перемещения? Что означают индексы при этих буквах? 2. Напишите общую формулу для определения перемещений (формулу Мора). Что означают входящие в нее величины? 3. Каков порядок вычисления перемещений по формуле Мора? 4. Назовите основные виды перемещений в плоских стержневых системах. Какая единичная сила, прикладываемая по направлению искомого перемещения, соответствует каждому из названных перемещений? 5. На что указывает положительный и на что отрицательный результат вычисленного перемещения? 6. Приведите пример на определение перемещения с применением правила Верещагина, в котором при перемещении эпюр площадь одной из них придется разбить на простые формулы. Вычислите это перемещение. 7. Когда при перемножении эпюр ставится знак плюс и когда — минус? К теме 3.8. 1.Какие системы называют статически неопределимыми? 2. В чем их преимущества и в чем недостатки? 3. Как определяется степень статической неопределимости различного вида систем? 4. Каков смысл понятия «лишние связи»? 5. В чем сущность расчета статически неопределимых систем методом сил? 6. Какую мысль выражает то или иное каноническое уравнение метода сил? 7. Как записывают канонические уравнения? 8. Какие требования предъявляют к выбору основной системы? 9. Какие способы, упрощающие расчет, можно применить к симметричной статически неопределимой раме и в чем их сущность? 10. В чем заключаются упрощения в результате использования рациональной основной системы? 11. Почему при деформационной проверке окончательной эпюры моментов путем ее перемножения с любой из единичных эпюр должен получиться нуль? 12. В чем заключается расчет рам с помощью таблиц?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАЧ КОНТРОЛЬНОЙ РАБОТЫ №1 ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Рекомендуется прочитать общие методические указания, прежде чем приступить к выполнению контрольной работы. К задаче 1 В задаче требуется определить силы в стержнях фермы аналитическим и графическим способами. К решению задачи можно приступить только после изучения тем «Основные понятия и аксиомы статики», «Плоская система сходящихся сил».
Аналитический способ решения. При расчете многостержневых конструкций (ферм) необходимо ввести обозначения стержней и узлов. Обычно стержни обозначают цифрами, узлы (места соединения двух или нескольких стержней) — буквами. Так. на рис. 1 узлы обозначены буквами А, В, С, D, Е, стержни — цифрами 1, 2, 3, 4, 5, 6, 7. Порядок обозначения стержней и узлов может быть произвольным. Определение сил в многостержневых конструкциях производится последовательным вырезанием узлов. Рассматривая узел как систему сходящихся сил, пользуясь уравнениями равновесия этой системы nx = 0, nу = 0, необходимо помнить, что, решая эти уравнения,, можно определить только две неизвестные силы. Это условие определяет порядок вырезания узлов. Первым рассматривается узел, в котором сходятся два стержня. Таким на рис. 1 является узел С. Прежде чем приступить к расчетам, конструкцию необходимо представить в виде расчетной схемы.
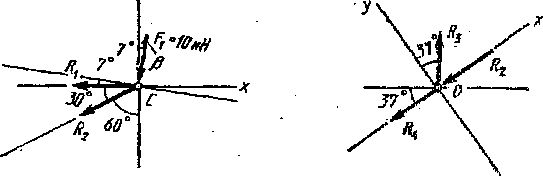 Покажем расчетную схему узла С на отдельном, рисунке (рис. 2). Она должна быть вычерчена аккуратно и чётко с нанесенными на нее силами, с указанием углов. Изображенная на рис. 2 расчетная схема узла С получена следующим образом. Покажем расчетную схему узла С на отдельном, рисунке (рис. 2). Она должна быть вычерчена аккуратно и чётко с нанесенными на нее силами, с указанием углов. Изображенная на рис. 2 расчетная схема узла С получена следующим образом.
Вырезаем узел С, для чего мысленно отбрасываем связи, заменив действие стержней реакциями R1 и R2 Реакция стержня направлена по его оси. Приложим к узлу С действующие на него силы: При расчетах ферм принято предполагать, что стержень растянут; в таком случае реакция направлена от рассматриваемой точки. Если же в результате решения та или иная из них получится отрицательной, то это значит, что предположенное направление данной реакции неправильное и следовательно, стержень не растянут, а сжат. Для равновесия узла необходимо, чтобы алгебраическая сумма проекций всех приложенных к нему сил на любые две непараллельные оси порознь равнялась нулю. Напоминаем, что проекция силы на ось равна взятому с соответствующим знаком произведению силы на косинус острого угла между линией действия силы и осью проекции. Заметим, что если оси проекций взаимно перпендикулярны, то не обязательно вычислять оба угла между линией действия силы и каждой осью проекций. В этом случае проекцию силы на одну ось можно вычислять как произведение силы на косинус острого угла между линией действия силы и данной осью, а проекцию этой же силы на другую ось — как произведение силы на синус того же угла. Направим ось х по реакции Угол между реакциями Из АКС следует; tg = АК/КС = 0, 5/4 = 0, 125 и =7°. Из ВКС: tg (+) = ВК/КС = 3/4 = 0, 75 и + = 37е Таким образом, угол = 30°. Угол между 1)
Из второго уравнения определяем R2 = - Из первого уравнения определяем
Знак минус у значения Силы в стержнях - соответственно равны Для определения сил в стержнях 3 и 4 вырезаем узел D. Расчетная схема узла D изображена на рис. 3. Направление неизвестных реакций Угол между горизонтом и направлением силы
Из второго уравнения В результате Графический способ решения. Определим этим способом силы в стержнях 1 и 2. Из трех сил, действующих на узел С, известна сила Мысленно перенеся направление найденных реакций на соответствующие стержни схемы конструкции, видим, что сила
К задачам 2 К решению любой из этих задач можно приступать после проработки тем «Пара сил» и «Плоская система произвольно расположенных сил».
 и и 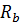 , поскольку в данной задаче, кроме сосредоточенного момента внешние нагрузки только вертикальные. Для удобства расчета равномерно распределенную нагрузку заменяем равнодействующей , поскольку в данной задаче, кроме сосредоточенного момента внешние нагрузки только вертикальные. Для удобства расчета равномерно распределенную нагрузку заменяем равнодействующей 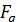 , которая равна произведению интенсивности q (кН/м)на длину участка ее приложения, т.е. , которая равна произведению интенсивности q (кН/м)на длину участка ее приложения, т.е. 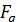 =qI =10 =qI =10 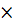 3 =30кН. Линия действия равнодействующей проходит через середину участка, занятого равномерно распределенной нагрузкой. 3 =30кН. Линия действия равнодействующей проходит через середину участка, занятого равномерно распределенной нагрузкой.
На расчетной схеме балки(рис.7, б) должны быть проставлены расстояния от сил до каждой из опор. Особое внимание обратите на расположение распределенной нагрузки на балках с консолями, чтобы избежать ошибок, часто возникающих при определении плеча силы Эти уравнения:
Так как определение реакций — первый этап расчета балки на изгиб, то его следует считать особенно ответственным. Поэтому во избежание ошибок при вычислении необходимо производить проверку найденных значений реакций. Составим уравнение проекций всех сил на ось у
Если это равенство не удовлетворяется, следовательно, при определении опорных реакций была допущена ошибка. б) Консольная балка (рис. 8, а). Балка с защемленной опорой называется консолью. Защемляющая неподвижная опора лишает балку всех трех степеней свободы: линейных перемещений вдоль осей х и у и возможности поворота в плоскости этих осей. Соответственно в защемлении появляются три неизвестные реакции:
1.Уравнение моментов сил относительно точки заделки Ма = 0 —для определения реактивного момента 2. 3. По расчетной схеме балки (рис. 8, б) составим уравнения равновесия
Значение Из уравнения Из уравнения Для проверки решения удобно составить уравнение моментов относительно произвольно взятой точки, например В:
Реакции вычислены правильно. К задаче 3. Перед тем как приступить к решению соответствующей задачи, следует изучить тему «Центр, тяжести», твердо усвоить понятие статического момента, знать положение центров тяжести простейших геометрических фигур и уметь определить координаты центров тяжести сложных сечений, представляющих собой совокупность простейших геометрических фигур, а также сечении, составленных из стандартных профилей проката (в последнем случае Необходимо уметь пользоваться таблицами ГОСТов), приведенными в приложениях 1—4. Знания и навыки по данной теме потребуются при изучении темы 2.4 «Геометрические характеристики плоских сечении». а)Определение координат центра тяжести сечения геометрической формы рассмотрим на примере (рис. 9). Приложение центра тяжести фигуры сложной формы можно определить, разбив эту фигуру на пять элементов простой формы, положения центров тяжести которых известны: I. прямоугольник 25X30 см с центром тяжести II. прямоугольник 55ХЮ см с центром тяжести III. прямоугольник 25X45 см с центром тяжести IV. два треугольника с центрами тяжести Нанесем на сечение координатные оси. Ось у совместим с осью симметрии сечения. Ось к проводим перпендикулярно ей по нижней грани сечения. Поскольку сечение симметрично относительно вертикальной оси и, следовательно, Определяем площади составных частей фигуры и координаты их центров тяжести относительно выбранной оси, исходя из размеров сечения. I. II. III. IV. Находим статический момент площади сечения
Площадь сечения А = Итак, точка С имеет координаты 0; 40, 5. По найденной ординате наносим на рисунок сечения точку С — центр тяжести. Разбивку рассмотренной фигуры по элементам можно было произвести иначе, как и положение оси х могло быть другим. б)Определение положения центра тяжести сечения, составленного из прокатных профилей, рассмотрим на примере (рис. 10). Простые элементы подобных сечений — стандартные профили прокатной стали: швеллер, двутавр, полоса, равнобокие и неравнобокие уголки. Все необходимые размеры и характеристики профилей приведены в таблицах ГОСТа (см. приложения 1—4), называемых сортаментом прокатных профилей. Порядок решения тот же, что в предыдущей задаче.
Разбиваем сечение на шесть составных частей и обозначаем их центры тяжести. Положение центра тяжести прокатного профиля принять по сортаменту: I. двутавр № 20 с центром тяжести II. швеллер № 20 с центром тяжести III. два неравнобоких уголка № 8/5 с общим центром тяжести IV. две полосы 12 200 мм с общим центром тяжести Положение координатных осей принимаем следующим образом: ось х совмещаем с осью симметрии сечения, следовательно, I. II. III. IV. Полная площадь сечения А= Находим статический момент сечения
Определяем координату центра тяжести
Итак, точка С имеет координаты 9, 04; 0. Наносим найденный центр тяжести на рисунок сечения.
|

 и N для рам? 5. Как проверить правильность построения эпюр
и N для рам? 5. Как проверить правильность построения эпюр 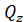
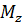 и N для статически определимых рам?
и N для статически определимых рам?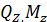 и N при действии на арку сосредоточенных сил недостаточно определить значение. этих внутренних силовых факторов в начале и конце каждого участка, чего, как известно, достаточно для построения эпюр для балок с прямой осью?
и N при действии на арку сосредоточенных сил недостаточно определить значение. этих внутренних силовых факторов в начале и конце каждого участка, чего, как известно, достаточно для построения эпюр для балок с прямой осью?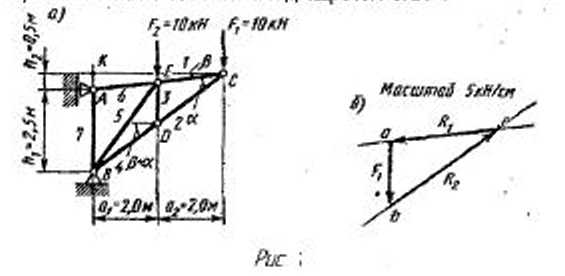
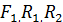 . Из них:
. Из них:  — активная сила, внешняя нагрузка, известная по модулю и направлению;
— активная сила, внешняя нагрузка, известная по модулю и направлению; 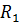 и
и 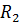 — численно неизвестные реакции связей, направленные вдоль стержней, но пока неизвестно в какую сторону.
— численно неизвестные реакции связей, направленные вдоль стержней, но пока неизвестно в какую сторону.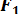 и осью у равен углу =7° как углы с взаимно перпендикулярными сторонами. Составим уравнения равновесия
и осью у равен углу =7° как углы с взаимно перпендикулярными сторонами. Составим уравнения равновесия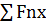 = 0; 2)
= 0; 2) 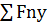 = 0 системы сил, сходящихся в узле С:
= 0 системы сил, сходящихся в узле С: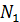 =
= 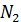 =
= 
 принимаем от узла, считаем, что стержни растянуты. Силу
принимаем от узла, считаем, что стержни растянуты. Силу 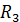 , - также 37. Рассматривая узел в состоянии равновесия, составим уравнение проекций всех действующих сил на оси:
, - также 37. Рассматривая узел в состоянии равновесия, составим уравнение проекций всех действующих сил на оси: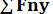 =
= 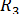 COS 37° = 0.
COS 37° = 0.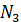 =
=  5 кН/см) и строим силовой треугольник (см. рис. 1, б). Из произвольной точки в принятом масштабе откладываем отрезок ab, равный силе
5 кН/см) и строим силовой треугольник (см. рис. 1, б). Из произвольной точки в принятом масштабе откладываем отрезок ab, равный силе 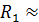 16 Кн,
16 Кн,  =
= 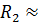 20 Кн.
20 Кн.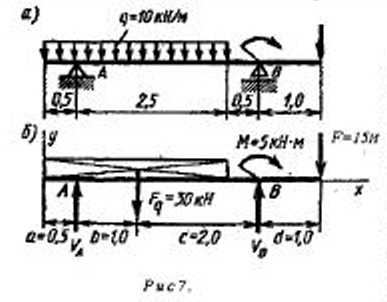 К задаче 2.Требуется определить значение опорных реакций балок двухопорной или жестко защемленной.
К задаче 2.Требуется определить значение опорных реакций балок двухопорной или жестко защемленной.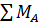 =
= 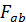 +M -
+M - 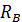 (b+c)+F(b+c+d)=0;
(b+c)+F(b+c+d)=0; =
= 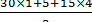 =31, 7кН;
=31, 7кН;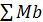 =
= 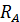 (b+c)-FqC+M+Fd=0;
(b+c)-FqC+M+Fd=0;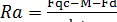 =
= 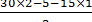 =13, 3кН.
=13, 3кН. -
- 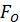 +
+ 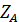 и реактивный момент заделки
и реактивный момент заделки 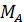 (рис. 8, 6). Для их определения наиболее удобными являются следующие уравнения равновесия
(рис. 8, 6). Для их определения наиболее удобными являются следующие уравнения равновесия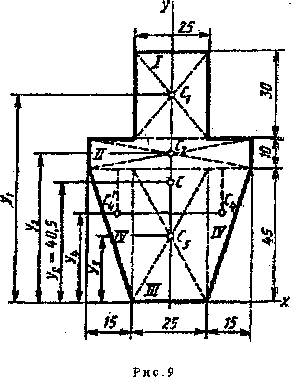

 , так как силы
, так как силы  и
и  , приложенные к точке А, в уравнение не войдут (их моменты относительно точки А равны нулю).
, приложенные к точке А, в уравнение не войдут (их моменты относительно точки А равны нулю). = 0 — для определения вертикальной реакции
= 0 — для определения вертикальной реакции  = О — для определения горизонтальной реакции
= О — для определения горизонтальной реакции 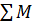 = -
= - 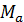 +
+  =
= 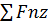 = 0 следует, что
= 0 следует, что  ;
;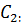
 ;
; .
.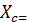 0, потребуется определить только ординату
0, потребуется определить только ординату 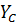 центра тяжести по формуле
центра тяжести по формуле 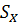 /A, где А — площадь сечения;
/A, где А — площадь сечения; 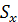 — статический момент сечения относительно оси х, определяется как сумма произведений площадей простых фигур на ординаты их центров тяжести.
— статический момент сечения относительно оси х, определяется как сумма произведений площадей простых фигур на ординаты их центров тяжести. = 25 30 = 750 см2,
= 25 30 = 750 см2,  = 70 см;
= 70 см;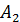 = 55 10 = 550 см, _
= 55 10 = 550 см, _ 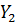 = 50 см;
= 50 см; = 25 45 = 1125
= 25 45 = 1125 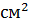
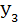 =22, 5 см;
=22, 5 см; ’ = 15 45/2 = 337, 5
’ = 15 45/2 = 337, 5 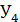 =
= 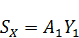 +
+ 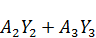 +2
+2 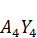 =750 70+550 50+1125 32, 5+2 33, 7 30=125562, 5
=750 70+550 50+1125 32, 5+2 33, 7 30=125562, 5 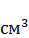
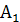 +
+ 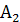 +
+ 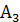 + 2
+ 2  = 750 + 550 + 1125 + 337, 5 2 = 3100
= 750 + 550 + 1125 + 337, 5 2 = 3100 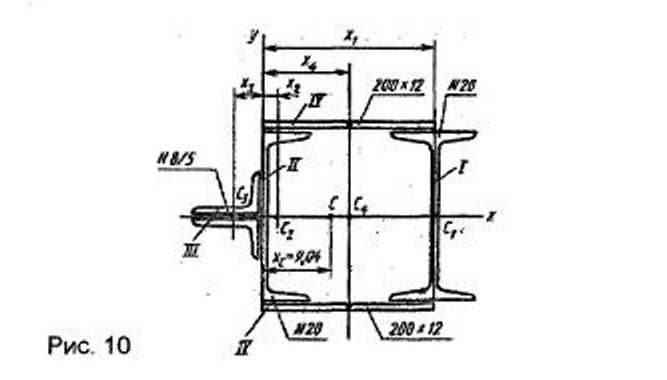
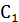 ;
; ,
,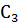 ;
;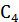 .
.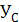 = 0; ось у проводим перпендикулярно оси х по наружной грани стенки швеллера. Необходимо определить лишь координату центра тяжести
= 0; ось у проводим перпендикулярно оси х по наружной грани стенки швеллера. Необходимо определить лишь координату центра тяжести 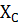 по формуле
по формуле 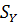 /A, где
/A, где 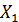 ,
, 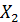 ,
, 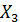 ,
,  центров тяжести прокатных профилей. Выписываем из соответствующих таблиц сортамента площади профилей и, используя размеры, находим абсциссы их центров тяжести:
центров тяжести прокатных профилей. Выписываем из соответствующих таблиц сортамента площади профилей и, используя размеры, находим абсциссы их центров тяжести: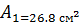 ,
, 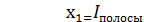 -20см;
-20см;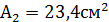 ,
, 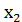 =
= 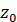 =2, 07 см (см.приложение 2);
=2, 07 см (см.приложение 2); =-2, 65см (см. приложение 4);
=-2, 65см (см. приложение 4);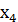 =-
=- 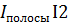 =10см.
=10см. .
.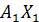 +
+  +
+ 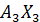 +
+  = 26, 8 20 + 23, 4 2, 07 + 15, 1 (-2, 65) +48 10 = 1024, 42
= 26, 8 20 + 23, 4 2, 07 + 15, 1 (-2, 65) +48 10 = 1024, 42 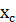 =
=  /113, 3
/113, 3 


