К задаче 3
Условие задачи. Определить силы в стержнях статически определимой фермы (рис. 16, а) путем построения диаграммы Максвелла — Кремоны. Решение. Чертеж фермы необходимо' выполнить, четко соблюдая заданные размеры в принятом масштабе. Приложим заданные внешние силы
Выбираем масштаб сил. Например, 5 кН/см (5 кН в одном см). От произвольной точки а в принятом масштабе откладываем внешнюю силу а — b(рис.16, б), затем b — с; от точки с вертикально вверх откладываем реакцию с — е. Так как сумма значений сил Построение диаграммы начинаем с узла С, где сходятся лишь два стержня. Стержни этого узла расположены между полями: двумя буквенными и одним цифровым. На силовой линии есть уже точки, соответствующие буквенным полям. Проводим через точку с прямую, параллельную стержню с — I, а через точку b — прямую, параллельную стержню 1 —b. Пересечение этих линий дает точку 1, соответствующую внутреннему полю между рассматриваемыми стержнями и примыкающему к рассматриваемому узлу. Строим точку 2. Стержни с —2 и 2-1 принадлежат узлу D, который можно вырезать, так как силы в двух стержнях неизвестны, а в третьем — найдены при рассмотрении первого_узла. Из точки 1 диаграммы проводим линию, параллельную стержню 2.— 1, а из точки С — линию, параллельную с —2. Точка 2 совпадает с точкой 1. Это означает, что сила в стержне 2— 1 равна нулю. Вырезаем узел Е, где сходятся четыре стержня, в двух из них силы можно определить по диаграмме, а в двух (2—3 и 3 — а) неизвестны. Строим точку 3. Для этого из точки 2 проводим прямую, параллельную стержню 2 — 3, а из точки а — параллельную 3 — а. На их пересечении получаем точку 3. Значения сил в стержнях определяем, измеряя длины линии на диаграмме с учетом принятого масштаба сил. Знак силы определяется следующим образом. Начнем с узла С, обходя его по часовой стрелке. Прочитывая на диаграмме обозначение стержня 1 —b, делаем движение по линии, обозначающей силу в стержне от одной точки к другой в соответствии с назначением. Это движение переносим на стержень фермы, совмещая начало движения с рассматриваемым узлом. Если движение при этом направлено по стержню от узла, стержень считается растянутым, а если к узлу — то сжатым. Итак, 1 — b —от узла, стержень растянут, N = 16 кН; с—1—к узлу, стержень сжат, ; N = — 20 кН; 1 - 2 стержень не - работает, N =0; с—2 — к. узлу, стержень сжат, N — 20 кН, 2—3 — к узлу, стержень сжат, N — 13 кН; 3 – а — от узла, стержень растянут N = 24 кН и т. д.
|

 и
и  и опорные реакции
и опорные реакции  и
и 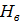 - Плоскость чертежа между внешними приложенными силами — внешние поля, обозначим а, b, с, е, d, обходя ферму по часовой стрелке. Плоскость чертежа, ограниченную стержнями, — внутренние поля обозначим цифрами 1, 2, 3. В дальнейшем каждую внешнюю и внутреннюю силы будем обозначать двумя значками, соответствующими наименованию тех смежных полей, границами которых они являются, называя эти буквы в порядке обхода фермы по часовой стрелке. Так, сила
- Плоскость чертежа между внешними приложенными силами — внешние поля, обозначим а, b, с, е, d, обходя ферму по часовой стрелке. Плоскость чертежа, ограниченную стержнями, — внутренние поля обозначим цифрами 1, 2, 3. В дальнейшем каждую внешнюю и внутреннюю силы будем обозначать двумя значками, соответствующими наименованию тех смежных полей, границами которых они являются, называя эти буквы в порядке обхода фермы по часовой стрелке. Так, сила 
 равна значению силы Vв, точка е совпадает с точкой а. Затем из точки е проводим прямую, параллельную
равна значению силы Vв, точка е совпадает с точкой а. Затем из точки е проводим прямую, параллельную  , и откладываем от нее реакцию е — d и, наконец, из точки d в обратном направлении откладываем реакцию d — a. В результате получаем замкнутый силовой многоугольник abceda. Далее, последовательно рассматривая узлы, строим диаграмму сил, возникающих в стержнях.
, и откладываем от нее реакцию е — d и, наконец, из точки d в обратном направлении откладываем реакцию d — a. В результате получаем замкнутый силовой многоугольник abceda. Далее, последовательно рассматривая узлы, строим диаграмму сил, возникающих в стержнях.


