Подбор сечения центрально – сжатой составной стойки
1. Задаются величиной коэффициента продольного изгиба 2. Определяют требуемую площадь поперечного сечения стойки
где N – центрально-сжимающая сила, Ry – расчетное сопротивление материала сжатию. 3. По найденной площади определяют номера профилей проката, из которых состоит сечение. В рамках расчетной работы рекомендуется принять профили одинаковыми по площади, если их несколько. 4. Проверяют устойчивость принятого сечения в следующем порядке: а) определяют расчетную длину стержня
где l – геометрическая длина стержня; б) определяют моменты инерции сечения в) определяют радиусы инерции сечения относительно осей х и у: ix= г) определяют гибкости стержня:
д) по наибольшему значению
Если это условие удовлетворено, то устойчивость стержня обеспечена, если не удовлетворено – не обеспечена. Если несущая способность стойки не обеспечена, то необходимо увеличить площадь сечения, приняв больший профиль, и выполнив проверку устойчивости стойки, добиваясь, чтобы напряжение было меньше расчетного сопротивления. Если напряжение в стойке равно расчетному сопротивлению или немного меньше, то сечение считается рационально подобранным, т.е. экономичным. Если напряжение намного меньше расчетного сопротивления, то такое сечение не экономично, так как имеет большой запас прочности. Поэтому, если недонапряжение составляет более 5%, то следует уменьшить площадь сечения (или увеличить гибкость) стойки, добиваясь, чтобы недонапряжение не превышало 5%. В некоторых случаях этого не удается добиться из-за ограниченности сортамента профилей проката. Пример№1
Решение: 1. Задаемся величиной 2. Определяем требуемую площадь сечения Принимаем все профили одинаковыми по площади. На один профиль требуется площадь 52, 8: 3=17, 6 Принимаем два швеллера №14а площадью 3. Проверим устойчивость принятого сечения стержня в следующем порядке: а) определим расчетную длину стержня где б) определяем моменты инерции сечения относительно осей х и у: 4
Тогда
Минимальный момент инерции в) определяем минимальный радиус инерции сечения г) определяем гибкость стержня
д) определяем действительное значение коэффициента
e) определяем действительное напряжение в подобранном сечении
Это недопустимо, поэтому необходим перерасчет. 1. Принимаем во втором приближении среднее значение коэффициента и между тем, которым задались, и тем, что получили:
2. Требуемая площадь сечения
На один профиль требуется 54, 3: 3=18, 1 Принимаем два швеллера №16 с Полная площадь сечения А=36, 2+17, 4=53, 6 3. Проверим устойчивость стойки а) б) поскольку
в) радиус инерции
г) гибкость стержня
д) коэффициент продольного изгиба получим интерполяцией между
е) действительное напряжение равно
ж) недонапряжение равно
Так как недонапряжение незначительно отличается от 5%, то расчет на этом заканчиваем.
Подобрать сечение центрально-сжатой стойки, если N=650 kH – нагрузка расчетная. L=5м; Ry=230Мпа Решение: 1. Задаемся величиной 2. Определяем требуемую площадь сечения На один уголок приходится площадь 47, 7: 4=11, 78 3. Проверим устойчивость принятого сечения в следующем порядке: а) Определяем расчетную длину стержня
где б) Определяем моменты инерции сечения относительно осей х и у:
Минимальный момент инерции в) Определяем минимальный радиус инерции сечения
г ) Определяем гибкость стержня д) Определяем действительное значение коэффициента
е) Действительное напряжение равно
Недонапряжение равно
Большое недонапряжение, требуется перерасчет. 1. Принимаем во втором приближении среднее значение коэффициента между тем, которыми задались, и тем, что получили:
2. Требуемая площадь сечения
На один профиль требуется 42, 9: 4=10, 73 Принимаем 4 неравнополочных уголка 100 3. Проверим устойчивость стержня:
б) поскольку
г) гибкость стержня
д) коэффициент продольного изгиба получим интерполяцией между
е) действительное напряжение равно
ж) недонапряжение равно
Для проверки возьмем 4 уголка 100 А=9, 59 Минимальный момент инерции
Радиус инерции
Гибкость стержня
Коэффициент продольного изгиба
Действительное напряжение равно
Окончательно принимаем 4 неравнополочных уголка 100
|

 . В первом приближении его можно принять равным
. В первом приближении его можно принять равным 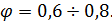


 - коэффициент проведения длины, который зависит от способа закрепления концов.
- коэффициент проведения длины, который зависит от способа закрепления концов.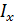 и
и  относительно главных центральных осей х и у, которые совпадают с осями симметрии сечения. Моменты инерции профилей проката относительно собственных осей определяют по таблице ГОСТов.
относительно главных центральных осей х и у, которые совпадают с осями симметрии сечения. Моменты инерции профилей проката относительно собственных осей определяют по таблице ГОСТов. iy=
iy=  ;
;
 y=
y= 
 ;
;
 Подобрать сечение центрально – сжатой стойки, если N=850kH – нагрузка расчетная l=4.Ry=230 Мпа
Подобрать сечение центрально – сжатой стойки, если N=850kH – нагрузка расчетная l=4.Ry=230 Мпа 
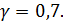

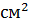
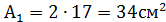 и двутавровую балку №14 площадью
и двутавровую балку №14 площадью 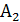 =17, 4
=17, 4 
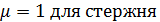 с шарнирным закреплением концов.
с шарнирным закреплением концов.
 =
= 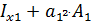 ; где
; где  =
= 
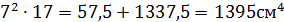
 ; где
; где  как ось х всего сечения совпадает с осью
как ось х всего сечения совпадает с осью  двутавра
двутавра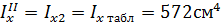


 =
=  где
где  так как оси у и
так как оси у и  совпадают.
совпадают.
 =
=  =
= 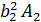


 =1132
=1132 
 см
см



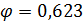
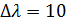






 =18, 1
=18, 1  и двутавровую балку №14 с
и двутавровую балку №14 с 
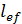 =4м осталось прежним
=4м осталось прежним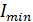 , то определим
, то определим 
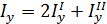
 =
=  =747
=747 









 Пример №2
Пример №2
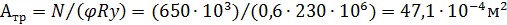 =47, 1
=47, 1  неравнополочных уголка 110
неравнополочных уголка 110  .
.




 =
= 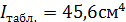


 =4
=4 

 =
= 



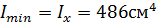
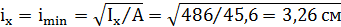






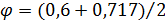 =0, 659
=0, 659


 то определим
то определим 
 =
= 

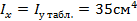



 = 3, 03 см
= 3, 03 см





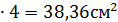


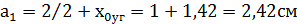
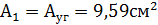






 МПа что недопустимо.
МПа что недопустимо.



