В тех случаях, когда физическая величина не может быть измерена непосредственно, прибегают к косвенным измерениям. Пусть 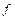 является некоторой функцией
является некоторой функцией  и
и  , т. е.
, т. е.  . Тогда наиболее точное значение при оценке
. Тогда наиболее точное значение при оценке 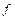 равно
равно  , где
, где  и
и  находятся по формуле (2). Как же найти
находятся по формуле (2). Как же найти  , если известны
, если известны  и
и  ? Так как сами величины
? Так как сами величины  и
и  находятся путем прямых измерений, то их абсолютные погрешности
находятся путем прямых измерений, то их абсолютные погрешности  и
и  можно оценить по формулам (4) и (5). Заметим, что
можно оценить по формулам (4) и (5). Заметим, что  ; следовательно, оценкой для
; следовательно, оценкой для  является разность:
является разность:
 , (7)
, (7)
т. е. ошибка косвенного измерения находится через ошибки прямых измерений по правилу дифференцирования. Поскольку погрешности всегда складываются, формулу (7) следует записать в виде:
 . (8)
. (8)
Более точным является следующее выражение:
 , (10)
, (10)
где  и
и 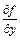 – частные производные по переменным
– частные производные по переменным  и
и  , взятые при значениях
, взятые при значениях  ;
;  .
.

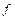 является некоторой функцией
является некоторой функцией  и
и  , т. е.
, т. е.  . Тогда наиболее точное значение при оценке
. Тогда наиболее точное значение при оценке  , где
, где  и
и  находятся по формуле (2). Как же найти
находятся по формуле (2). Как же найти  , если известны
, если известны  и
и  ? Так как сами величины
? Так как сами величины  ; следовательно, оценкой для
; следовательно, оценкой для  , (7)
, (7) . (8)
. (8) , (10)
, (10) и
и 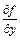 – частные производные по переменным
– частные производные по переменным  ;
;  .
.


