НАПРЯЖЕНИЯ ПО НАКЛОННЫМ СЕЧЕНИЯМ ПРИ ОСЕВОМ РАСТЯЖЕНИИ ИЛИ СЖАТИИ

Добавлено admin в Июль 21, 2010

Правильно оценить опас­ность, угрожающую прочности стержня, можно, лишь зная полно­стью его напряженное состояние, а это требует уменья вы­числять напряжения не только по сечению, перпенди­кулярному к оси, а по любому.

Вычислим напряжения, действующие по какому-либо наклонному сече­нию. Возь­мем призматический стержень, растянутый силами Р (рис. 11.1). Раз­делим его на две части: I и II сечением тп, составляющим угол a с попереч­ным сечением mk, перпен­дикулярным к оси. Тот же угол составляют между собой и нормали к этим сечениям.

 

За положительное направление отсчета этого угла возьмем направ­ление против часовой стрелки. Нормаль ОА, направлен­ную на­ружу по отношению к отсеченной части стержня, будем называть внешней нормалью к сечению тп. Площадь сечения mk обозначим F_o, пло­щадь же сечения тп обозначим F_a.

Для нахождения напряжений, передающихся через намеченное сечение от верхней (I) части на нижнюю (II), отбросим мысленно верхнюю часть и заменим действие ее на нижнюю напряжениями р_a.

Для равновесия нижней части напряжения р_a должны уравнове­шивать силу Р и быть направлены параллельно оси стержня. В дан­ном случае на­пряжения уже не перпендикулярны к той площадке, по которой они дейст­вуют. Величина их тоже будет иной, чем для площадки mk.

Сделав предположение, что в достаточном удалении от мест при­ложения внешних сил Р напряжения р_a равномерно распределены по площади на­клонного сечения тп, найдем

Но так как F_a=F/cos a, тгде s₀=P/F_o – нормальное напряжение по площадке mk, перпендикуляр­ной к растягивающей силе.

При изменении угла a меняется и величинапол­ных напряжений р_а, дейст­вующих по проведенной площадке. Чтобы при лю­бом угле наклона а иметь дело всегда с одними и теми же видами напряже­ний, разложим напряжения р_а на две составляющие: в плоскости тп и перпенди­кулярно к ней (рис. 11.2). Та­ким образом, напряжение р_а, действующее в точке А площадки тп, мы заменяем двумя взаимно перпенди­кулярными напряжениями: нормальным напряже­нием s_а и касательным напряжением t_a.

Величины этих двух напряжений будут меняться в зависимости от изме­нения угла а между нормалью к площадке и нап­равлением растягивающей силы. Из рис. 11.2 имеем

s_a= p_a× cosa=s₀× cos²a, (1).

t_a= p_a× sina=s₀× sina× cosa= 0, 5s₀× sin2a. (2).

Установим следующие условия относительно знаковнапряжений s_a и t_a. Растягивающиенапряжения s_a, т. е. совпадающие с на­правлением внешней нормали, будем считать положительными; нор­мальные напряжения обрат­ногонаправления – сжимающие– будем принимать со знаком минус.

Касательноенапряжение будем считать положительным, если при пово­роте вектора t против часовой стрелки на 90° его направле­ние совпадет с на­правлением внешней нормали. Обратное направ­ление t будем считать отри­цательным.

На рис. 11. 3 показаны принятые условия относительно знаков a и t.

При любом угле наклона площадки a мы всегда будем иметь дело лишь с двумявидами напряжений, действующих в каждой точке проведенного разреза: с нормальным и касательным напряже­ниями.

На рис. 11.4 показано действие этих напряжений на тонкий слой материала (на рисунке заштрихованный), выделенный из растяну­того стержня двумя параллельными сечениями 1 – 1 и 2 – 2. К каж­дой из плоскостей приложены и нормальные растягивающие напря­жжения s_a, и касательные t_a, вызываю­щие сдвиг сечений 1 – 1 и 2 – 2, параллельно одно другому.

Таким образом, наличие двух видов напряжений приводит к двум видам деформации: удлинению (или укорочению) и деформации сдвига. Этому со­ответствуют и два вида разрушения материала – путем отрыва и путем сдвига, что наблюдается и в опытах на рас­тяжение.

Для проверки прочности материала стержня необходимо найти наи­большиезначения напряжений s_a и t_a, величины которых зави­сят от поло­жения площадки тп.

Из формул (1) и (2) следует, что s_a достигает своего наиболь­шего значе­ния, когда cos²a будет равен единице и угол a=0. Мак­симум же t_a получится при sin2a=l, т. е. при 2a=90° и a=45°. Величины этих наибольших напряже­ний будут равны

 

7. Закон Гука при сдвиге: g = t/G или t = G× g.

G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).

Потенциальная энергия при сдвиге: .

Удельная потенциальная энергия деформации при сдвиге: ,

где V=а× F — объем элемента. Учитывая закон Гука, .

Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.

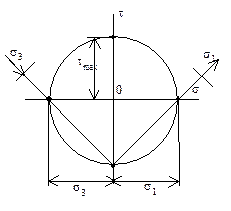Круг Мора при чистом сдвиге.