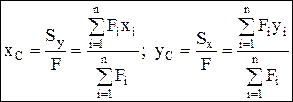Площадь:  , dF — элементарная площадка.
, dF — элементарная площадка.
 Статический момент элемента площади dF относительно оси 0x — произведение элемента площади на расстояние " y" от оси 0x: dSx = y× dF
Статический момент элемента площади dF относительно оси 0x — произведение элемента площади на расстояние " y" от оси 0x: dSx = y× dF
Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и x: 
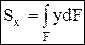 ;
; 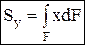 [см3, м3, т.д.].
[см3, м3, т.д.].
Координаты центра тяжести:  . Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями Fi и координатами центров тяжести xi, yi.Статический момент площади всей фигуры = сумме статических моментов каждой ее части:
. Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями Fi и координатами центров тяжести xi, yi.Статический момент площади всей фигуры = сумме статических моментов каждой ее части:  .
.
Координаты центра тяжести сложной фигуры: 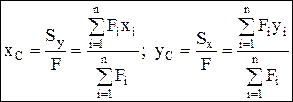

 , dF — элементарная площадка.
, dF — элементарная площадка. Статический момент элемента площади dF относительно оси 0x — произведение элемента площади на расстояние " y" от оси 0x: dSx = y× dF
Статический момент элемента площади dF относительно оси 0x — произведение элемента площади на расстояние " y" от оси 0x: dSx = y× dF
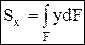 ;
; 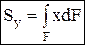 [см3, м3, т.д.].
[см3, м3, т.д.]. . Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями Fi и координатами центров тяжести xi, yi.Статический момент площади всей фигуры = сумме статических моментов каждой ее части:
. Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями Fi и координатами центров тяжести xi, yi.Статический момент площади всей фигуры = сумме статических моментов каждой ее части:  .
.