Пенроуз Р. 2 страница
Ответ: 43, 3 м.
94. Снаряд вылетел из пушки под углом a к горизонту с начальной скоростью uо. Найти: · зависимость координат снаряда от времени и получить уравнение траектории; · время полета снаряда; · максимальную высоту подъема снаряда; · дальность полета снаряда; · под каким углом к горизонту нужно вести стрельбу, чтобы при заданной начальной скорости дальность полета снаряда была наибольшей? · под каким углом к горизонту нужно вести стрельбу, чтобы высота подъема снаряда была равна дальности его полета? Ответ: у = tqa× x - g/(2uо2cos2a)× x2, t = (2uоsina)/g, h = (uо2sin2a)/2g, S = (uо2sin2a)/g, 45о, 76о.
95. Камень брошен с башни под углом 30о выше уровня горизонта со скоростью 10 м/с. Каково расстояние между местом бросания камня и местом его нахождения спустя 4 с после момента его бросания? Ответ: 69, 3 м.
96. На крутом берегу реки высотой 200 м находится орудие, ствол которого расположен на 30о ниже уровня горизонта. Известно, что скорость вылета снаряда 500 м/с. На какое расстояние от берега надо подпустить вражескую лодку, чтобы поразить ее? Ответ: 346, 6 м.
97. Из шланга, лежащего на земле, бьет под углом 45о к горизонту вода с начальной скоростью 10 м/с. Площадь сечения шланга 5 см2. Определить массу струи, находящейся в воздухе. Ответ: 7 кг.
98. Два камня брошены под различными углами к горизонту со скоростями u1 и u2 так, как показано на рисунках (а) и (б). Не прибегая к расчетам, сделать вывод, какой камень улетит дальше. Ответ: в обоих случаях первый.
99. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом 60о к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1, 7 с. Ответ: 22 м.
100. Мяч, брошенный с земли со скоростью 10 м/с под углом 45о к горизонту, упруго ударяется о вертикальную стенку, находящуюся на расстоянии 3 м от места бросания. Определить: а) модуль и направление скорости мяча после удара; б) на каком расстоянии от места броска мяч упадет на землю. Ответ: а) 7, 63 м/с; 22о выше уровня горизонта; б) 4 м.
101. Какое расстояние по горизонтали пролетит тело (до удара о пол), брошенное со скоростью 10 м/с под углом 60о к горизонту, если оно упруго ударяется о потолок? Высота потолка 3 м. Ответ: 4, 8 м.
102. Под углом 60о к горизонту брошено тело с начальной скоростью 20 м/с. Спустя какое время оно будет двигаться под углом 45о к горизонту? Ответ: 0, 73 с; 2, 7 с.
103. Из орудия ведут обстрел объекта, расположенного на склоне горы. На каком расстоянии от орудия будут падать снаряды, если их начальная скорость 100 м/с, угол наклона горы 30о (ниже уровня горизонта), а ствол орудия расположен горизонтально? Ответ: 1333 м.
104. Из орудия ведут обстрел объекта, расположенного на склоне горы. На каком расстоянии от орудия будут падать снаряды, если их начальная скорость 100 м/с, угол наклона горы 30о, угол стрельбы 60о по отношению к горизонту? Ответ: а) 667 м, если наклон горы вверх к горизонту, б)1333 м, если наклон горы вниз к горизонту.
105. На какое максимальное расстояние можно забросить тело вверх на наклонную плоскость с углом 30о выше уровня горизонта, если начальная скорость тела 10 м/с? Ответ: 6, 7 м.
106. Тело А бросают вертикально вверх со скоростью 20 м/с. На какой высоте h находилось тело Б, которое, будучи брошено с горизонтальной скоростью 4 м/с одновременно с телом А, столкнулось с ним в полете? Расстояние по горизонтали между исходными положениями тел равно 4 м. Найти также время движения тел до столкновения и скорость каждого тела в момент столкновения. Ответ: h = 20 м; uА = 10 м/с, uБ = 10, 8 м/с, t = 1 с.
107. С башни высотой 10 м в горизонтальном направлении бросают камень со скоростью 23 м/с. Одновременно с поверхности земли под углом 30о к горизонту бросают камень со скоростью 20 м/с навстречу первому. На каком расстоянии от башни находится точка бросания второго камня, если камни столкнулись в воздухе? Ответ: 40, 4 м.
108. Параллельно поверхности земли летел коршун со скоростью 5 м/с. Царевич пустил стрелу со скоростью 15 м/с, прицелившись прямо в коршуна под углом 60о к горизонту. На какой высоте летел коршун, если стрела попала в него? Ответ: 7, 5 м.
109. С аэростата, поднимающегося с ускорением 0, 5 м/с2, через 4 с после его отрыва от земли бросают под углом 30о к горизонту камень со скоростью 5, 5 м/с относительно аэростата. На каком расстоянии от места подъема аэростата с земли камень упадет на землю? Сколько времени камень будет находиться в полете? Ответ: 7, 2 м; 1, 5 с.
110. Шарик свободно падает по вертикали на наклонную плоскость. Пролетев расстояние 1 м, он упруго отражается и второй раз падает на ту же плоскость. Найти расстояние между точками соприкосновения шарика и плоскости, если плоскость составляет с горизонтом угол 30о. Ответ: 4 м.
111. Ответ: tga = H/L, a = arctg(H/L) = 58о.
Кинематика движения по окружности
112. Точка равномерно движется по окружности радиуса 1, 2 м и за 1 мин совершает 24 оборота. Найти: период, частоту, угловую скорость линейную скорость и центростремительное ускорение точки. Ответ: 2, 5 с; 0, 4 с-1; 2, 5 рад/с; 3 м/с; 7, 5 м/с2.
113. За 10 с точка прошла половину окружности, радиус которой 1 м. Определить ее линейную скорость. Ответ: 0, 314 м/с.
114. Точка движется по окружности с постоянной скоростью 0, 5 м/с. Вектор скорости изменяет свое направление на 30о за каждые 2 с. Каково нормальное ускорение точки? Ответ: 0, 13 м/с2.
115. Конец минутной стрелки часов на Спасской башне Кремля передвинулся за 1 мин на 37 см. Какова длина стрелки? Ответ: 3, 5 м.
116. Минутная стрелка часов в три раза длиннее секундной. Каково отношение линейных скоростей концов этих стрелок? Ответ: 1: 20.
117. Каково ускорение точек земного экватора, обусловленное суточным вращением Земли? Ответ: 0, 034 м/с2.
118. Определить линейную скорость точки поверхности Земли, соответствующей широте г. Кирова (58о северной широты), и на экваторе. Ответ: 246, 5 м/с, 465, 2 м/с.
119. На сколько орбита первого спутника Земли короче орбиты третьего спутника, если средние радиусы их орбит отличаются на 410 км? Ответ: 2574, 8 км.
120. Точка движется в плоскости, причем ее прямоугольные координаты определяются уравнениями x = Aсos(wt), y = Asin(wt), где А и w - постоянные. Какова траектория точки? Ответ: окружность радиуса А с центром в начале координат.
121. Две точки М и К движутся по окружности с постоянными угловыми скоростями wм = 0, 2 рад/с и wк = 0, 3 рад/с. В начальный момент времени угол между радиусами этих точек равен p/3. В какой момент времени точки первый раз встретятся? Ответ: 52, 3 с.
122. По окружности радиуса 2 м одновременно движутся две точки так, что уравнения их движения имеют вид: j1 = 2 + 2t и j2 = -3 – 4t. Определить их относительную скорость в момент встречи. Ответ: 12 м/с.
123. Ответ: 1 с-1.
124. Мальчик вращает камень, привязанный к веревке длиной 0, 5 м, в вертикальной плоскости с частотой 3 об/с. На какую высоту взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх? Ответ: 4, 5 м относительно места обрыва веревки.
125. Определить радиус маховика, если при вращении скорость точек его на ободе 6 м/с, а скорость точек, находящихся на 15 см ближе к оси, 5, 5 м/с. Ответ: 1, 8 м.
126.
Автомобиль А движется по закруглению радиусом 0, 5 км, а автомобиль В – прямолинейно. Расстояние АВ = 200 м. Скорость каждого автомобиля 60 км/ч. Найти скорость автомобиля В относительно автомобиля А в указанный момент времени. Ответ: -24 км/ч, т.е. направлена назад.
127. Пропеллер самолета радиусом 1, 5 м вращается с частотой 2× 103 об/мин, при этом посадочная скорость самолета относительно земли равна 161 км/ч. Какова скорость точки на конце пропеллера? Какова траектория движения этой точки? Ответ: 317 м/с, винтовая линия радиусом 1, 5 м с шагом 1, 34 м.
128. Тело брошено горизонтально со скоростью 4 м/с с высоты 1 м. Определить радиусы кривизны траектории в ее начальной и конечной точках. Ответ: 1, 6 м, 5, 4 м.
129. Колесо застрявшей в грязи машины вращается с частотой 2 об/с. Радиус колеса 60 см. На каком наименьшем расстоянии от центра колеса должен стоять человек, чтобы в него не попадали комья грязи? Ответ: 6, 2 м.
130. Ответ: uА = 0, uВ = 4 м/с, uС = 2, 83 м/с, uD = 2ucos(a/2), uЕ = 2usin(a/2).
131. Ответ: а) катушка покоится; б) вправо; в) влево.
132. Ответ: u0R/(R-r).
133. Решить предыдущую задачу, если нить сматывается с катушки так, как показано на рисунке. Ответ: u0R/(R+r).
134. Ответ: 5 м.
135. Ответ:
136. Ответ: 1 м/с.
137. Ответ: 5 м/с.
138. Цилиндр радиусом 25 см зажат между движущимися со скоростями u1 = 6 м/с и u2 = 4 м/с параллельными рейками. С какой угловой скоростью вращается цилиндр? Ответ: 20 рад/с.
139. Обруч, проскальзывая, катится по горизонтальной поверхности. В некоторый момент времени скорость верхней точки А равна 6 м/с, а нижней точки В - 2 м/с. Определить скорость концов диаметра СD, перпендикулярного к АВ для того же момента времени. Ответ: 4, 47 м/с.
140. Ответ: w = (u1+u2)/(R+r), uо = (u1R-u2r)/(R+r).
141. Ответ: 1, 35 м/с, 0, 15 м/с.
142. Точка, лежащая на пересечении рельса с внешним ободом колеса поезда, движется в данный момент времени со скоростью u = 5 м/с. С какой скоростью и в каком направлении движется поезд, если r = 50 см, R = 56 см. Ответ: 10 м/с, вправо.
Равнопеременное движение по окружности 143. Вал начинает вращение из состояния покоя и в первые 10 с совершает 50 оборотов. Считая вращение вала равноускоренным, определить угловое ускорение. Ответ: 6, 3 рад/с2.
144. Шкив радиусом 20 см приводится во вращение грузом, подвешенным на нити, сматывающейся со шкива. В начальный момент времени груз был неподвижен, а затем стал опускаться с ускорением 2 см/с2. Найти угловую скорость шкива в тот момент, когда груз пройдет 1 м и ускорение точек, лежащих на поверхности шкива. Ответ: 1рад/с; 0, 2 м/с2.
145. Материальная точка, начав двигаться равноускоренно по окружности радиусом 1 м, прошла за 10 с 50 м. С каким нормальным ускорением двигалась точка спустя 5 с после начала движения? Ответ: 25 м/с2.
146. Точка движется по окружности радиусом 20 см с постоянным тангенциальным ускорением. Найти величину этого ускорения, если известно, что к концу пятого оборота после начала движения линейная скорость точки 79, 2 cм/с. Ответ: 0, 05 м/с2.
147. Точка движется по окружности радиуса 20 см с постоянным касательным ускорением 5 см/с2. Через сколько времени после начала движения нормальное ускорение будет равно касательному? Ответ: 2 с.
148. Тело начинает вращаться с постоянным угловым ускорением 0, 04 рад/с2. Через сколько времени после начала вращения полное ускорение какой-либо точки тела будет направлено под углом 76о к направлению скорости этой точки? Ответ: 10 с.
149. Диск начинает движение из состояния покоя и вращается равноускоренно. Каким будет угол между вектором скорости и вектором ускорения произвольной точки диска, когда он сделает один оборот? Ответ: 85о.
150. Машина въезжает со скоростью 36 км/ч на закругленный участок шоссе радиусом 200 м и начинает тормозить с ускорением 0, 3 м/с2. Найти нормальное и полное ускорение машины, а также угол между ними через 30 с после указанного момента. Ответ: аn = 5 мм/с2, а = 0, 3 м/с2, j = 89о.
151. Поезд въезжает на закругленный участок пути с начальной скоростью 54 км/ч и проходит путь 600 м за 30 с, двигаясь равноускоренно. Радиус закругления равен 1 км. Определить скорость и ускорение в конце этого пути. Ответ: 90 км/ч, 0, 71 м/с2.
152. Ступенчатый шкив с радиусами r = 0, 25 м и R = 0, 5 м приводится во вращение грузом, опускающимся с ускорением 2 см/с2. Определить модуль и направление ускорения точки М в тот момент, когда груз пройдет путь 100 см. Ответ: ам = 32 м/с2, 83о к вертикали.
153. Снаряд вылетел со скоростью 320 м/с, сделав внутри ствола два оборота. Длина ствола 2 м. Считая движение снаряда внутри ствола равноускоренным, найти его угловую скорость вращения вокруг оси в момент вылета из ствола. Ответ: 2013 рад/с.
154.
Диск радиусом 1 м начинает движение из состояния покоя и вращается равноускоренно. Тангенциальное ускорение точки, лежащей на ободе диска, 0, 04 м/с2. Через сколько времени ускорение этой точки будет направлено под углом 45о к ее скорости? Ответ: 5 с.
155. Ответ: uА = 0, uВ = 4 м/с, uС = uD = 2, 83 м/с; а А = 4 м/с2, а В = 5, 66 м/с2, а С = 6, 32 м/с2, а D = 2, 83 м/с2.
Динамика
Законы Ньютона. Движение без учета трения 156. Могут ли силы F1 = 10 Н и F2 = 14 Н, приложенные к одной точке, дать равнодействующую, равную 2 Н; 4 Н; 10 Н; 24 Н; 30 Н? Ответ: 4 Н £ F £ 24 Н; 2 Н и 30 Н не могут.
157. Найти равнодействующую сил 2 Н, 4 H и 5 Н, образующих между собою на плоскости последовательно прямые углы. Ответ: 5 Н.
158. Найти равнодействующую трех сил по 20 Н каждая, если углы между первой и второй, второй и третьей силами равны 60о. Ответ: 40 Н.
159. Три силы действуют вдоль одной прямой. В зависимости от направления этих сил, их равнодействующая может быть равна 1 Н, 2 Н, 3 Н и 4 Н. Чему равна каждая из этих сил? Ответ: 0, 5 Н, 1 Н, 2, 5 Н.
160. Два человека тянут шнур в противоположные стороны, каждый с силой 100 Н. Разорвется ли шнур, если он может выдержать нагрузку 150 Н? Ответ: Нет.
161. В каком случае натяжение троса будет больше: 1) два человека тянут трос за концы с силами F, равными по модулю, но противоположными по направлению; 2) один конец троса привязан к столбу, а другой конец человек тянет с силой 2F? Ответ: Во втором.
162. Под действием силы в 20 Н тело движется с ускорением 0, 4 м/с2. С каким ускорением будет двигаться это тело под действием силы в 50 Н? Ответ: 1 м/с2.
163. Некоторая сила сообщает первому телу ускорение 2 м/с2, а второму телу - ускорение 3 м/с2. Какое ускорение под действием той же силы получат оба тела, если их соединить вместе? Ответ: 1, 2 м/с2.
164. С какой силой нужно действовать на тело массой 5 кг, чтобы оно падало вертикально вниз с ускорением 15 м/с2? Ответ: 25 Н.
165. Поезд массой 500 т, двигавшийся по горизонтальному пути со скоростью 13 м/с, останавливается под действием постоянной силы сопротивления, равной 100 кН. Сколько времени длилось торможение? Ответ: 65 с.
166. Автомобиль массой 2 т, трогаясь с места, прошел путь 100 м за 10 с. Найти силу тяги двигателя, если сила сопротивления движению 1 кН. Ответ: 5 кН.
167. Космический корабль массой 106 кг поднимается с Земли вертикально вверх. Сила тяги двигателя равна 3× 107 Н. С каким ускорением поднимается корабль? Ответ: 20 м/с2.
168. Воздушный шар массой 160 кг опускается с постоянной скоростью. Какое количество балласта нужно выбросить, чтобы шар поднимался с той же скоростью? Подъемная сила воздушного шара равна 1400 Н. Ответ: 40 кг.
169. Человек массой 70 кг находится в лифте. Определить вес человека: 1) перед началом подъема; 2) в начале подъема с ускорением 3 м/с2; 3) в конце подъема с “замедлением” 3 м/с2. Ответ: 1) 700 Н; 2) 910 Н; 3) 490 Н.
170. Какую перегрузку испытывает водитель, если автомобиль с места набирает скорость 180 км/ч за 10 с? Ответ: Р/Ро = 1, 1.
171. Через сколько секунд тело, брошенное вертикально вверх со скоростью 44, 8 м/с, упало на землю, если сила сопротивления воздуха не зависела от скорости и составляла 1/7 силы тяжести? Ответ: 8, 6 с.
Движение со связями. 172. Грузы массами 0, 2 кг и 0, 3 кг, связанные тонкой нерастяжимой нитью, находятся на гладкой горизонтальной поверхности. С каким ускорением будут двигаться грузы и какова сила натяжения нити, если к грузу массой 0, 2 кг приложена горизонтальная сила 1 Н? Ответ: 2 м/с2; 0, 6 Н.
173. Два тела, связанные нитью, находятся на гладком горизонтальном столе. Когда сила 100 Н была приложена к правому телу, сила натяжения нити была 30 Н. Какой будет сила натяжения нити, если приложить эту силу к левому телу? Ответ: 70 Н.
174. Четыре одинаковых бруска связаны нитями и положены на гладкий горизонтальный стол. К первому бруску приложена сила F. Определить ускорения тел и силы натяжения нитей. Ответ: а = F/4m; Т1 = 3F/4, Т2 = F/2, Т3 = F/4.
175. На гладком горизонтальном столе лежит веревкамассой 1 кг. К ней прикладывают горизонтально направленную силу 2 Н. Найти силу натяжения веревки в сечении, находящемся на расстоянии 1/3 длины веревки от точки приложения силы. Ответ: 1, 33 Н.
176. К концам шнура, перекинутого через неподвижный блок, подвешены грузы 200 г и 300 г. Определить ускорения, с которыми будут двигаться грузы, силу натяжения шнура и показание динамометра, на котором висит блок. Ответ: 2 м/с2; 2, 4 Н, 4, 8 Н.
177. Найти ускорения тел массами m1 = 0, 1 кг и m2 = 0, 3 кг, а также силу натяжения нити. Массой блоков и нитей можно пренебречь. Ответ: а 1 = 2, 86 м/с2, а 2 = 1, 43 м/с2, Т = 1, 3 Н.
178. Ответ: а лев = 0, 5g; а сред = 0, 75g, а прав = g, Т = 0, 5 mg.
179. Ответ: 1, 125 м/с2.
180. Ответ: 5/9 м/с2.
181. К концам невесомой и нерастяжимой нити, перекинутой через неподвижный блок, подвешены два груза массой по 100 г каждый. На один из грузов положен перегрузок массой 10 г. Найти силу, с которой перегрузок давит не груз, а также силу давления на ось блока. Ответ: 0, 09 Н; 2, 056 Н.
182. Через неподвижный блок перекинута веревка, за концы которой одновременно хватаются две обезьяны массами 20 кг и 25 кг. Более легкая обезьяна держится за один конец веревки, а более тяжелая, схватившись за другой, карабкается вверх так, чтобы всё время оставаться на одной высоте. Через какое время более легкая обезьяна достигнет блока, если в начальный момент времени она находилась ниже оси блока на расстоянии 16, 6 м? Ответ: 3, 65 с.
183. Между двумя одинаковыми гладкими брусками массой 1 кг каждый вставлен равнобедренный клин массой 1 кг с углом при вершине a = 60о. Вся система находится на гладкой плоскости. Определить ускорения брусков и клина. Ответ: 3, 5 м/с2; 6 м/с2.
184. Ответ: 4, 2 м/с2, 3, 5 м/с2. Движение по окружности
|


 Из точки А свободно падает тело. Одновременно из точки В под углом a к горизонту бросают другое тело так, что оба тела столкнулись в воздухе. Определить угол a, если Н/L = 1, 6.
Из точки А свободно падает тело. Одновременно из точки В под углом a к горизонту бросают другое тело так, что оба тела столкнулись в воздухе. Определить угол a, если Н/L = 1, 6.
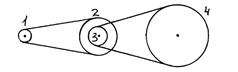 Движение от шкива 1 к шкиву 4 передается при помощи двух ременных передач. Шкивы 2 и 3 жестко укреплены на одном валу. Найти частоту вращения шкива 4, если шкив 1 делает 1200 об/мин, а радиусы шкивов: R1 = 8 см, R2 = 32 см, R3 = 11 см, R4 = 55 см.
Движение от шкива 1 к шкиву 4 передается при помощи двух ременных передач. Шкивы 2 и 3 жестко укреплены на одном валу. Найти частоту вращения шкива 4, если шкив 1 делает 1200 об/мин, а радиусы шкивов: R1 = 8 см, R2 = 32 см, R3 = 11 см, R4 = 55 см.
 Велосипедист едет с постоянной скоростью u = 2 м/с по прямолинейному участку дороги. Найти мгновенные скорости точек А, В, С, D и Е, лежащих на ободе колеса и указанных на рисунке.
Велосипедист едет с постоянной скоростью u = 2 м/с по прямолинейному участку дороги. Найти мгновенные скорости точек А, В, С, D и Е, лежащих на ободе колеса и указанных на рисунке. В какую сторону будет катиться катушка, если ее тянуть за нить под разными углами? Во всех случаях катушка не проскальзывает.
В какую сторону будет катиться катушка, если ее тянуть за нить под разными углами? Во всех случаях катушка не проскальзывает. Катушка с намотанной на нее нитью может катиться по поверхности горизонтального стола без скольжения. С какой скоростью и в каком направлении будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью u0? Радиус внутренней части катушки - r, внешней - R.
Катушка с намотанной на нее нитью может катиться по поверхности горизонтального стола без скольжения. С какой скоростью и в каком направлении будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью u0? Радиус внутренней части катушки - r, внешней - R.
 С колеса автомобиля, движущегося со скоростью 72 км/ч, летают комки грязи. Радиус колеса 40 см. На какую высоту над дорогой будет подбрасываться грязь, оторвавшаяся от т. А колеса, положение которой указано на рисунке? Угол j = 30о.
С колеса автомобиля, движущегося со скоростью 72 км/ч, летают комки грязи. Радиус колеса 40 см. На какую высоту над дорогой будет подбрасываться грязь, оторвавшаяся от т. А колеса, положение которой указано на рисунке? Угол j = 30о. С какой скоростью должен ехать автомобиль, чтобы оторвавшийся с его колеса в точке А камушек попал в ту же точку колеса, находящуюся в том же положении? Радиус колеса 20 см.
С какой скоростью должен ехать автомобиль, чтобы оторвавшийся с его колеса в точке А камушек попал в ту же точку колеса, находящуюся в том же положении? Радиус колеса 20 см. м/с, где k - целое число.
м/с, где k - целое число. Кривошип ОА, вращаясь с угловой скоростью 2, 5 рад/с, приводит в движение колесо радиуса r = 5 см, катящееся по неподвижному колесу радиуса R = 15 см. Найти скорость точки В.
Кривошип ОА, вращаясь с угловой скоростью 2, 5 рад/с, приводит в движение колесо радиуса r = 5 см, катящееся по неподвижному колесу радиуса R = 15 см. Найти скорость точки В. Диск зажат между движущимися со скоростями u1 = 6 м/с и u2 = 4 м/с параллельными рейками. Какова скорость центра диска?
Диск зажат между движущимися со скоростями u1 = 6 м/с и u2 = 4 м/с параллельными рейками. Какова скорость центра диска?

 Две нити, намотанные на катушку, тянут со скоростями u1 и u2. С какой скоростью движется центр катушки? С какой угловой скоростью вращается катушка? Радиусы r и R заданы.
Две нити, намотанные на катушку, тянут со скоростями u1 и u2. С какой скоростью движется центр катушки? С какой угловой скоростью вращается катушка? Радиусы r и R заданы. Шарик радиусом 5 см катится равномерно и без проскальзывания по двум параллельным рейкам, расстояние между которыми d = 6 см, и за каждые 2 с проходит 120 см. С какими скоростями движутся верхняя и нижняя точки шарика?
Шарик радиусом 5 см катится равномерно и без проскальзывания по двум параллельным рейкам, расстояние между которыми d = 6 см, и за каждые 2 с проходит 120 см. С какими скоростями движутся верхняя и нижняя точки шарика?


 Скорость центра колеса, катящегося без проскальзывания по горизонтальной поверхности, изменяется со временем по закону uо = 1 + 2t (м/с). Радиус колеса 1 м. Найти скорости и ускорения четырех точек, лежащих на ободе колеса на концах взаимно перпендикулярных диаметров, один из которых горизонтален, через 0, 5 с после начала движения.
Скорость центра колеса, катящегося без проскальзывания по горизонтальной поверхности, изменяется со временем по закону uо = 1 + 2t (м/с). Радиус колеса 1 м. Найти скорости и ускорения четырех точек, лежащих на ободе колеса на концах взаимно перпендикулярных диаметров, один из которых горизонтален, через 0, 5 с после начала движения.

 На рисунке изображена система движущихся тел. Наклонная плоскость составляет угол 30о с горизонтом. Определить ускорения тел и силу натяжения нити.
На рисунке изображена система движущихся тел. Наклонная плоскость составляет угол 30о с горизонтом. Определить ускорения тел и силу натяжения нити. В механической системе, изображенной на рисунке, грузы массами m1 = 5 кг и m2 = 4 кг лежат на горизонтальной поверхности. Невесомая и нерастяжимая нить охватывает три невесомых блока. На свободную ось верхнего блока начинает действовать постоянная вертикальная сила 10 Н. Определить ускорение верхнего блока. Трением пренебречь.
В механической системе, изображенной на рисунке, грузы массами m1 = 5 кг и m2 = 4 кг лежат на горизонтальной поверхности. Невесомая и нерастяжимая нить охватывает три невесомых блока. На свободную ось верхнего блока начинает действовать постоянная вертикальная сила 10 Н. Определить ускорение верхнего блока. Трением пренебречь.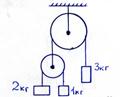
 Через неподвижный блок перекинута нить, на одном конце которой подвешена гиря массой 3 кг, а на другом конце - второй невесомый блок. На концах нити, перекинутой через второй блок, висят гири массой 2 кг и 1 кг. С каким ускорением будет двигаться гиря массой 3 кг?
Через неподвижный блок перекинута нить, на одном конце которой подвешена гиря массой 3 кг, а на другом конце - второй невесомый блок. На концах нити, перекинутой через второй блок, висят гири массой 2 кг и 1 кг. С каким ускорением будет двигаться гиря массой 3 кг?
 Найти ускорения призмы массой 1 кг и куба массой 2 кг, изображенных на рисунке. Трением пренебречь. Угол a = 40о.
Найти ускорения призмы массой 1 кг и куба массой 2 кг, изображенных на рисунке. Трением пренебречь. Угол a = 40о.


