Теоретические сведения. Логарифмом положительного числа по основанию (где ) называется показатель степени, в которую надо возвести
Логарифмом положительного числа Логарифм числа Если Например, Для обозначения десятичных логарифмов принята специальная запись: вместо Свойства логарифмов: 1. Логарифмы существуют только для положительных чисел, т.е. 2. При основании 3. При основании 4. Равным положительным числам соответствуют и равные логарифмы, т.е. если 5. Если 6. Если 7. Логарифм единицы по любому основанию ( 8. Логарифм самого основания равен 1, т.е. Пример 1. Вычислить: 1) Решение. 1) Нам известно, что логарифмом числа Таким образом, Решим уравнение Таким образом, 2) Пусть Чтобы решить полученное уравнение, необходимо упростить основания степеней, т.е. привести их к одному основанию:
Таким образом, наше уравнение примет вид Таким образом, Для решения остальных примеров используем основное логарифмическое тождество. 3) 4)
|

 по основанию
по основанию  (где
(где  ) называется показатель степени, в которую надо возвести
) называется показатель степени, в которую надо возвести  .
. , то
, то  есть тождество, которое называют основным логарифмическим тождеством.
есть тождество, которое называют основным логарифмическим тождеством. ,
,  .
. , где
, где  .
. (где
(где  .
. логарифмы чисел
логарифмы чисел  положительны, а логарифмы чисел
положительны, а логарифмы чисел  отрицательны.
отрицательны. логарифмы чисел
логарифмы чисел  , то
, то  .
. , то
, то  .
. , то
, то  .
. .
. .
. ; 2)
; 2) 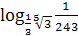 ; 3)
; 3)  ; 4)
; 4)  .
.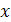 . Тогда
. Тогда  , или
, или  .
.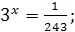
 т.е.
т.е.  .
. .
. , тогда
, тогда  .
. ,
, .
. . Так как
. Так как  ,
,  .
. .
. .
. .
.


