Пусть  и
и 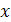 - произвольное иррациональное число. Рассмотрим последовательность
- произвольное иррациональное число. Рассмотрим последовательность  десятичных приближений числа
десятичных приближений числа 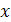 . Эта последовательность имеет предел
. Эта последовательность имеет предел  .
.
Можно показать, что последовательность  также имеет предел. Этот предел обозначают
также имеет предел. Этот предел обозначают  и называют степенью числа
и называют степенью числа  с показателем
с показателем 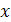 .
.
При любом  и любом
и любом  степень
степень  является положительным действительным числом:
является положительным действительным числом:  при
при  .
.
При таком определении степени с действительным показателем сохраняются все известные свойства степени с рациональным показателем.
Для любого  и любого
и любого  число
число  больше 1.
больше 1.
Теорема. Пусть  и
и  . Тогда
. Тогда  .
.
По условию  . Поэтому,
. Поэтому,  . Умножив обе части этого равенства на положительное число
. Умножив обе части этого равенства на положительное число  , получим
, получим  .
.
Отсюда по свойству умножения степеней получаем,  , т.е.
, т.е. 
Следствие 1. Пусть  и
и  . Тогда
. Тогда  .
.
Так как  , то
, то  . Поэтому из теоремы следует, что при
. Поэтому из теоремы следует, что при 
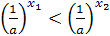 .
.
По свойству деления степеней 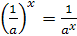 . Следовательно,
. Следовательно,  , откуда
, откуда  .
.
Следствие 2. Пусть  . Тогда
. Тогда  .
.
Предположим, что равенство  не выполняется. Пусть, например,
не выполняется. Пусть, например,  . Тогда при
. Тогда при  по теореме должно быть
по теореме должно быть  , а при
, а при  по следствию 1 должно быть
по следствию 1 должно быть  , что противоречит условию
, что противоречит условию  .
.

 и
и 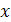 - произвольное иррациональное число. Рассмотрим последовательность
- произвольное иррациональное число. Рассмотрим последовательность  десятичных приближений числа
десятичных приближений числа  .
. также имеет предел. Этот предел обозначают
также имеет предел. Этот предел обозначают  и называют степенью числа
и называют степенью числа  с показателем
с показателем  и любом
и любом  при
при  .
. и любого
и любого  число
число  . Тогда
. Тогда  .
. . Поэтому,
. Поэтому,  . Умножив обе части этого равенства на положительное число
. Умножив обе части этого равенства на положительное число  , получим
, получим  .
. , т.е.
, т.е.  и
и  . Поэтому из теоремы следует, что при
. Поэтому из теоремы следует, что при 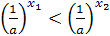 .
.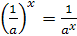 . Следовательно,
. Следовательно,  , откуда
, откуда  .
. . Тогда
. Тогда  .
. .
.


