Теоретические сведения. Рассмотрим степень , где – рациональное число
Рассмотрим степень Степень с рациональным показателем обладает теми же свойствами, что и степень с натуральным показателем, а именно если а) б) в) г) д) Пример 1. Упростить выражение: 1) Решение. 1) 2) 3) 4) 5) Пример 2. Вычислить: 1) Решение. 1) Освободимся от отрицательного показателя и упростим данное нам выражение:
2) Освободимся от отрицательных показателей и упростим данное нам выражение:
3) Освободимся от отрицательных показателей и упростим данное нам выражение:
Задание 1. Вычислите: 1) 2) 3) Задание 2. Выполнить указанные действия: 1) 2) 3) 4) 5) 6) 7) 8) Контрольные вопросы: 1. Дайте определение степени 2. Сформулируйте правила действия над степенями с рациональным показателем. Рекомендуемая литература: 1.1, 1.4, 2.1
|

 , где
, где  – рациональное число. Выражение
– рациональное число. Выражение  . Если
. Если 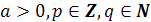 , то по определению
, то по определению  ;
; 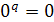 .
.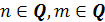 , то:
, то: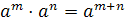 ;
; ;
; ;
; ;
; .
.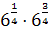 ; 2)
; 2) 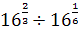 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 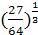 .
.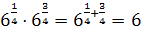 ;
; ;
;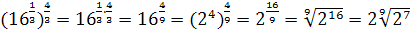 ;
;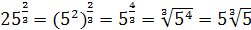 ;
; .
.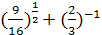 ; 2)
; 2)  ; 3)
; 3) 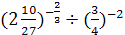 .
.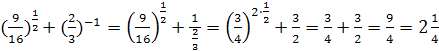 .
. .
. Задания к практической работе
Задания к практической работе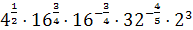 ;
; .
. .
. ;
;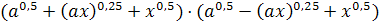 ;
;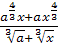 ;
;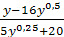 ;
; ;
;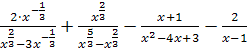 ;
; ;
; .
. .
.


