Пиранозные и фуранозные кольцевые структуры моносахаридов
Моносахариды с числом атомов углерода 5 и более существуют в растворе преимущественно в виде замкнутых циклических структур, причем их карбонильная группа находится не в свободном состоянии, а образует ковалентную связь с одной из гидроксильных групп, связанных с атомом углерода основной цепи. Довольно часто встречающиеся шестичленные циклические формы моноз, например, D-глюкозы, из-за их сходства с шестичленным гетероциклическим соединением пираном (рис. 7.3) получили название пираноз. Устойчивые пиранозные кольца могут образовывать только альдозы, содержащие пять и более атомов углерода. Однако многие гексозы и большинство пентоз существуют также в виде циклических соединений с пятичленными кольцами. Из-за сходства таких колец с пятичленным гетероциклическим соединением фураном (рис. 7.3) их называют фуранозами.
Рис. 7.3. Структурные формулы шести- и пятичленного гетероциклов – Для изображения циклических форм моносахаридов обычно пользуются так называемыми перспективными формулами Хеуорса. В таких формулах часть кольца, расположенную ближе к читателю, изображают жирными линиями (рис. 7.4). Примером может служить изображение шести- и пятичленного вариантов структуры глюкозы и фуранозной формы фруктозы с помощью перспективных формул Хеуорса (рис. 7.4). а) Рис. 7.4. Пиранозная и фуранозная перспективные формулы молекул D-глюкозы (а) и фуранозная форма молекулы D-фруктозы (б)
|

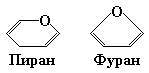
 б)
б) 



