Где X — некоторая постоянная, п — произвольное целое
Функции (7.35) имеют максимум прит — п/Х и нормированы. Второй случайный процесс в этой задаче, никак не связанный с первым, определяется последовательностью случайных событий — длительностями обслуживания каждого из покупателей. Распределение вероятностей длительности обслуживания имеет тот же качественный вид, что и в предыдущем случае. Для примера в таблице в колонке А записаны случайные числа — промежутки между приходами клиентов (в минутах), в колонке В — случайные числа — длительности обслуживания (в минутах). Для определенности взято атах = 10 и Ьтгх = 5. Из этой короткой таблицы, разумеется, невозможно установить, какие законы распределения приняты для величин А и В. Остальные колонки предусмотрены для удобства анализа; входящие в них числа находятся путем элементарного расчета. В колонке С представлено условное время прихода клиента; В — момент начала обслуживания; Е — момент конца обслуживания; Е — длительность времени, проведенного клиентом в системе в целом; С — время, проведенное в очереди в ожидании обслуживания; Н — время, проведенное системой в ожидании клиентов (если их нет). Таблицу удобно заполнять по горизонтали, переходя от строчки к строчке. Так как начало обслуживания очередного клиента определяется либо временем его прихода, если система не занята, либо временем ухода предыдущего клиента, приведем для удобства соответствующие формулы (в них / = 1, 2, 3,...): с, = 0, с/+1 = С/ + я/+1; < 1Х = 0, = шах(с/+1, е,); (7.36а) ех = Ьь е1 = 4 + Ъ» / = е, - с,; & = 0, =/+1 - 6/+1; А, = 0, йж = - е{. (7.366) Таким образом, при данных случайных наборах чисел в колонках А и В и клиентам приходилось стоять в очереди (колонка С), и система простаивала в ожидании клиента (колонка Н).
При моделировании систем такого вида прежде всего возникает вопрос, какое среднее время приходится стоять в очереди? Ответить на него, кажется, несложно — надо найти 1 = й+.» + &,) (7.37) п
в некоторой серии испытаний. Аналогично можно найти среднее значение величины А. Труднее ответить на вопрос о достоверности полученных результатов; для этого надо провести несколько серий испытаний и использовать стандартные методы математической статистики (часто уместна обработка с помощью распределения Стьюдента). Более сложный вопрос — каково распределение случайных величин Си Нпри заданных распределениях случайных величин А и В? Качественный ответ на него можно попытаться получить, построив соответствующие гистограммы по результатам моделирования. Затем делается некоторая гипотеза о виде распределения и используются один или несколько статистических критериев проверки достоверности этой гипотезы. Располагая функцией распределения (пусть даже эмпирической, но достаточно надежной), можно ответить на любой вопрос о характере процесса ожидания в очереди. Например: какова вероятность прождать дольше т минут? Ответ будет получен, если найти отношение площади криволинейной трапеции, ограниченной графиком плотности распределения, прямыми х=тиу = 0, к площади всей фигуры. Контрольные вопросы 1. Что такое «случайный процесс»? 2. Каковы принципы компьютерного генерирования равномерно распределенных случайных чисел? 3. Как можно получить последовательность случайных чисел с пуассоновским законом распределения? 4. Что такое «система массового обслуживания»? Приведите примеры. 5. В чем заключается метод Монте-Карло вычисления площадей плоских фигур? объемов тел? 6. Какие примеры случайных процессов Вы можете привести?
|

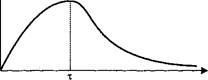 Рис. 7.6. Схематическое изображение плотности вероятности распределения времени между появлениями клиентов в системе массового обслуживания
Рис. 7.6. Схематическое изображение плотности вероятности распределения времени между появлениями клиентов в системе массового обслуживания



