Метод наименьших квадратов. Предположим, у нас имеется набор экспериментальных точек зависимости Y от X
Предположим, у нас имеется набор экспериментальных точек зависимости Y от X. Возникает вопрос, как по этим экспериментальным точкам наилучшим образом воспроизвести зависимость Y от X? Для решения подобных задач обычно применяется расчетный метод, известный под названием " Метод наименьших квадратов". Этот метод дает возможность при заданном типе зависимости Y=f(X) так выбрать ее числовые параметры, чтобы график зависимости Y=f(X) наилучшим образом отображал экспериментальные данные. Тип зависимости Y=f(X), как правило, выбирается исходя из внешнего вида полученного набора точек. Он может быть линейным, квадратичным, экспоненциальным и т.д.. В методе наименьших квадратов под условием «наилучшим образом» понимают следующее требование: " Сумма квадратов отклонений экспериментальных точек от сглаживающей кривой должна быть минимальной ". Рассмотрим линейную зависимость. Пусть имеется набор из n экспериментальных точек с координатами (х1, y1), (х2, у2),..., (хn, уn). Предполагается, что точки отображают линейную зависимость. Требуется подобрать по методу наименьших квадратов коэффициенты а и b линейной функции у = ах + b. Решение. Запишем у как функцию не только аргумента х, но и параметров а и b (так как величины а и b неизвестны): у = f (х; a, b) = ax + b (1) Требуется выбрать а и b так, чтобы выполнялось условие: " Сумма квадратов отклонений экспериментальных точек от построенной линейной зависимости должна быть минимальной", то есть для набора n экспериментальных точек должно быть выполнено условие:
или
где уi - значение у-координаты i-ой точки из набора экспериментальных точек, хi - значение x-координаты i-ой точки из набора экспериментальных точек, (ахi + b) - значение функции у = ах + b в i-ой точке. Найдём значения а и b, при которых левая часть выражения (2) обращается в минимум. Для этого продифференцируем её по а и b; приравняем производные нулю:
где Система уравнений (3) содержит столько уравнений, сколько неизвестных коэффициентов в искомой зависимости. В нашем случае их два – а и b. Продифференцируем (1) по а и b, получим:
(4)
Подставим выражения (4) в (3) и получим два уравнения для определения а и b:
(5)
Раскроем скобки, просуммируем и получим:
Получили систему из двух уравнений с двумя неизвестными, которая легко решается. Рассмотрим теперь конкретный пример. Пусть имеется набор из 3 экспериментальных точек с координатами (1, 1), (2, 2) и (3, 0). Предполагается, что точки отображают линейную зависимость. Требуется найти коэффициенты а и b для линейной функции у = ах + b. Решение.
Воспользуемся системой уравнений (6) и подставим в неё координаты экспериментальных точек. Получаем следующую систему уравнений:
Решаем и получаем a = -0.5, b = 2. Таким образом, вид линейной функции: у = - 0.5 х + 2.
Под интерполяцией понимают построение гладкой функции, проходящей через все заданные точки. Для этого применяют интерполяционные кубические сплайны, NURBS-сплайны, B-сплайны и т.п.
|

 (2)
(2)
 ;
;  (3)
(3) - значение частной производной функции у(х) = ах + b по параметру а в точке c координатами (хi, уi), а
- значение частной производной функции у(х) = ах + b по параметру а в точке c координатами (хi, уi), а  - значение частной производной функции по параметру b.
- значение частной производной функции по параметру b. ;
; 
 ;
; 
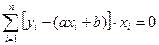

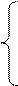
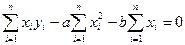 (6)
(6) , где n – число точек
, где n – число точек