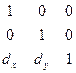Однородные координаты. Однородными координатами точки называется тройка одновременно не равных нулю чисел

Однородными координатами точки называется тройка одновременно не равных нулю чисел.

В компьютерной графике однородные координаты вводятся так: произвольной точке Р(х, у) на плоскости ставится в соответствие точка Р(х, у, 1) в пространстве.

Соединим прямой точки О(0, 0, 0) и Р(х, у, 1). Любую точку этой прямой, соединяющей начало системы координат О(0, 0, 0) с точкой Р(х, у, 1), можно задать тройкой чисел (hx, hy, h), где h≠ 0. Проведём плоскость z = 1, параллельную плоскости ху, через точку Р(х, у, 1). Прямая, соединяющая точки О и Р, пересекает плоскость z = 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху. Таким образом, между произвольной точкой с координатами (х, у) и множеством троек чисел (hx, hy, h), где h≠ 0, устанавливается взаимно однозначное соответствие, позволяющее считать числа hx, hy, h новыми (однородными) координатами этой точки. В компьютерной графике вслед за проективной геометрией для однородных координат принято обозначение:

х: у: 1

или в более общем случае:

х₁: х₂: х₃ (числа х_1, х₂, х₃ не должны быть равны нулю одновременно).

Однородные координаты удобны для программирования геометрических преобразований. При помощи однородных координат и матриц 3-го порядка можно выполнить любое геометрическое преобразование в плоскости. Любое геометрическое преобразование выполняется следующим действием:

(x', y', 1) = (x, y, 1)

x'=x a +y c +1 e; y'=x b +y d +1 f

Для каждого геометрического преобразования существует своя матрица.

Рассмотрим конкретный пример сдвига. На ху-плоскости есть точка Р с координатами (1, 1). Требуется сдвинуть (перенести) эту точку на 1 единицу по оси х и на 5 единиц по оси у. Для сдвига существует следующее матричное выражение:

(x', y', 1) = (x, y, 1)

Здесь d_x =1, d_y =5. Следовательно, получаем: x'=1× 1+1× 0+1× 1=2; y'=1× 0+1× 1+1× 5=6