Сплайны
Сплайн - кусочный полином степени K с непрерывной производной степени K-1 в точках соединения сегментов.
Далее нас будут интересовать кубические сплайны.
Понятие сплайна пришло из машиностроения, где сплайном называли гибкую линейку, закрепив которую в нужных местах, добивались плавной кривой, которую затем чертили по этой линейке (см. Рис. 7) Форма такой линейки, если ее рассматривать как функцию y(x), будет удовлетворять уравнению Эйлера-Бернулли:
1) Для N отрезков имеем 4N коэффициентов: 2) Условия 3) Требование 4) Требование
Итого имеем 4N-2 уравнения; для того чтобы система была определенной, необходимы еще 2 уравнения; их можно вывести, например, из заданных значений производных на границах или из условия периодичности. При корректно заданных условиях линейная относительно
|
, где M(x) - момент изгиба вдоль рейки, E - модуль Юнга. зависящий от свойств материала рейки, I - момент инерции, определяемый формой кривой. Если мы фиксируем некоторые точки подпорками, то момент изгиба на каждом отрезке 
меняется по линейному закону: M(x) = A*x + B, подставляя в исходное уравнение получаем: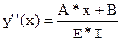 
, дважды интегрируя получаем уравнение кривой на данном
Рис. 7. Сплайн.
; таким образом форма физического сплайна описывается кусочным кубическим полиномом.
Теперь рассмотрим задачу построения системы таких кубических полиномов для всего отрезка 
для 
;
(i Î 
) дают 2N уравнений;
в точках 
(i Î 
) дает N-1 уравнений;
в точках 
система имеет единственное решение. Подробнее смотри в Ошибка! Источник ссылки не найден..
