Понятие тесноты связи
Заметим, что сдвиг b нельзя считать объективной характеристикой зависимости Y от X, потому что его величина определяется выбором начала координат. Из соотношения (5), в частности, следует, что для МНК-оценок
Это соотношение связывает отклонения оценки отклика и фактора от их выборочных средних значений. Переход от величин к их отклонениям от среднего называется центрированием этих величин. Заметим, что значение На первый взгляд кажется, что по величине коэффициента
где введено обозначение:
Величина r называется выборочным коэффициентом корреляции (см. Приложение). Коэффициент r показывает, на сколько значений sy в среднем увеличится отклик, если фактор увеличится на sx. Говорят, что выборочный коэффициент корреляции характеризует тесноту связи между X и Y. Известно, что | r | ≤ 1. Чем ближе | r | к 1, тем теснее связь между X и Y; чем ближе | r | к 0, тем слабее связь. При r =±1 точки наблюдений лежат на прямой, задаваемой соотношением (2). При r =0 прямая (2) параллельна оси абсцисс, и связь между X и Y отсутствует. Примеры тесной и слабой связи даны на рис.2.
|

 прямая, задаваемая уравнением (2), всегда проходит через точку (
прямая, задаваемая уравнением (2), всегда проходит через точку ( ). Подставив (5) в (2), после несложных преобразований получим:
). Подставив (5) в (2), после несложных преобразований получим: . (6)
. (6)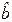 в соотношении (6) не присутствует.
в соотношении (6) не присутствует.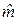 можно судить о степени зависимости Y от X: чем больше
можно судить о степени зависимости Y от X: чем больше  sx (sy). Разделим обе части соотношения (6) на sy, а затем правую часть умножим и разделим на sx. Тогда получим:
sx (sy). Разделим обе части соотношения (6) на sy, а затем правую часть умножим и разделим на sx. Тогда получим: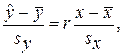 (7)
(7)