Оценивание параметров уравнения линейной регрессииДля получения оценок Обозначим: Графически определение остатков поясняется на рис. 1. Координатная плоскость, на которой нанесены точки наблюдений, называется полем корреляции. С учетом принятых обозначений остаточная сумма является суммой квадратов остатков и задается формулой:
Ясно, что чем меньше Qe, тем лучше оценки соответствуют наблюдениям. Из необходимого условия экстремума Qe (равенства частных производных по
В формулах (4) и (5) использованы обозначения: Определения перечисленных выше выборочных характеристик приводятся в Приложении. Вывод формул (4) и (5) дается, например, в [5].
|
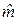и 
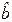традиционно используется метод наименьших квадратов (МНК). В соответствии с МНК значения 
– оценка отклика для i -го наблюдения, i =1, …, n; 
– отклонение наблюдения отклика от оценки; величины ei называются остатками; Qe – остаточная сумма.
(3)
и 
нулю) можно получить формулы для оценок параметров уравнения линейной регрессии:
, (4)
. (5)
– выборочная ковариация переменных X и Y, 
– выборочная дисперсия переменной X, 
и 
– выборочные средние значения X и Y, соответственно.
