Уравнение парной линейной регрессии
Пусть функционирование экономического объекта описывается двумя числовыми переменными: входной переменной X и выходной переменной Y. Возможно, что X может изменяться (регулироваться) исследователем, а значение Y получается как результат функционирования объекта. Предполагается, что Y зависит от X практически линейно: Y = mX + b +e, (1) где m и b – детерминированные величины, e – случайная величина. Выходная переменная Y называется зависимой переменной (или объясняемой переменной, или откликом). Входная переменная X называется независимой переменной (или объясняющей переменной, или фактором, или регрессором). Случайную величину e в эконометрике называют возмущением. Если математическое ожидание возмущения равно нулю, то функция f (x)= mx + b является условным математическим ожиданием Y при заданном значении X=x: f (x)≡ MxY. В этом случае соотношение (1) называется регрессионным уравнением. Чтобы подчеркнуть, что переменных всего две, а связь между ними линейная, говорят, что (1) – уравнение парной линейной регрессии. Функция f (x) называется регрессией (линейной) Y по X (или функцией регрессии), а величины m и b – параметрами линейной регрессии (m – коэффициентом, b – сдвигом). Пусть имеется n наблюдений величин X и Y: (x1, y1), (x2, y2), …, (xn, yn). Из соотношения (1) получаем: yi = mxi + b +ε i, где ε i – возмущение в i -ом наблюдении, i =1, …, n. Требуется по наблюдениям найти в некотором смысле наилучшие оценки
Формулу (2) можно использовать для прогноза значения отклика по интересующему исследователя значению фактора.
|

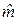 и
и 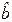 значений m и b. Если
значений m и b. Если  по известному значению фактора x можно определить по формуле:
по известному значению фактора x можно определить по формуле: . (2)
. (2)


