Проверка гипотезы о коэффициенте линейной регрессииКоэффициент m незначим, если m =0; в этом случае Y не зависит от X, и изменение Y обусловлено только случайной составляющей ε. Проверим гипотезу H: m =0. Оценка
Так как оценки
имеет распределение Стьюдента с (n -2) степенями свободы. Если гипотеза Н верна, то
и большие по модулю значения статистики (15в) маловероятны. Поэтому при выполнении неравенства | T |> t (a; n- 2), (16) где t (a; n- 2) – квантиль распределения Стьюдента уровня 1-a, гипотезу Н следует отклонить. Вероятность ошибки первого рода при использовании правила (16) равна a. Для парной регрессии F =
|
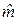имеет (см. §1.4) нормальное распределение с математическим ожиданием 
и дисперсией 
: 
. Для приведения этого распределения к стандартному нормальному надо разность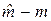 
разделить на 
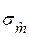. При вычислении 
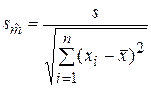(15а)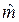
и s независимы, то статистика
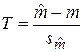(15б)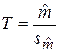
, (15в)
