Получение оценок параметров линейной регрессии
Статистическая функция ЛИНЕЙН вычисляет МНК-оценки параметров и другие характеристики линейной регрессии. Последовательность работы с этой функцией: 1. Выделите область пустых ячеек из пяти строк и двух столбцов (5´ 2), в которую будут выведены результаты. 2. Вызовите окно функции ЛИНЕЙН (например, из главного меню выберите Вставка/Функция, а в полученном окне мастера функций – ЛИНЕЙН). 3. В окне функции ЛИНЕЙН укажите (с помощью мыши) значения аргументов: Известные_значения_ y – диапазон с числовыми данными отклика (добычи угля на одного рабочего); Известные_значения_x – диапазон с числовыми данными фактора (толщины пласта); Константа – значение 1 или пустое поле, если сдвиг b вычисляется обычным способом, или значение 0, если предполагается b =0; Статистика – значение 1, если выводятся все результаты (заполняются все десять выделенных ячеек), или значение 0, если выдаются только оценки параметров регрессии (два значения в первой из выделенных строк). 4. Закончите вызов функции нажатием комбинации клавиш Ctrl+Shift+Enter. В выделенную область результаты будут записаны, как указано в таблице 2:
Таблица 2. Схема расположения результатов функции ЛИНЕЙН
|
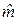– оценка коэффициента регрессии
– оценка сдвига
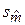– выборочное среднее квадратическое отклонение 
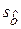– выборочное среднее квадратическое отклонение 
Результаты функции ЛИНЕЙН для наших данных приведены в таблице 3. Таким образом,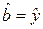 
при x =0, а значение x =0 далеко отстоит от наблюдений фактора.
