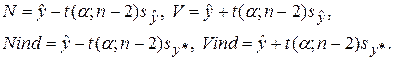Выполнение задания в среде Excel
Доверительный интервал коэффициента регрессии определяем по формуле (18). В практической работе №1 уже нашли:  1, 02, 1, 02, 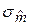 =0, 207 (см. таблицу 3); t (0, 05; 8)=2, 31 (с помощью функции СТЬЮДРАСПОБР). Подставив эти значения в формулу (18), получаем 95-процентный доверительный интервал для коэффициента m: 0, 538≤ m ≤ 1, 495. =0, 207 (см. таблицу 3); t (0, 05; 8)=2, 31 (с помощью функции СТЬЮДРАСПОБР). Подставив эти значения в формулу (18), получаем 95-процентный доверительный интервал для коэффициента m: 0, 538≤ m ≤ 1, 495.
Для расчета интервальной оценки дисперсии возмущений в формулу (19) подставляем значение Qe =8, 39 из таблицы 3. Квантили распределения хи-квадрат находим, применяя функцию ХИ2ОБР: c2(0, 025; 8)=17, 53, c2(0, 975; 8)=2, 18. Получаем 95-процентный доверительный интервал дисперсии возмущений: 0, 479≤ s2≤ 3, 85.
Расчеты доверительных границ функции регрессии и индивидуальных значений отклика приведены в таблице 5. Рассматривался немного более широкий диапазон x, чем диапазон наблюдений. Значения 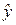 вычислялись по формуле (2), вычислялись по формуле (2),  – по формуле (20), sy * – по формуле (23). Значения – по формуле (20), sy * – по формуле (23). Значения 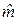 , , 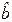 , , 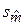 , s были взяты из таблицы 3. Через N (V) обозначена нижняя (верхняя) доверительная граница функции регрессии, через N инд (V инд) –нижняя (верхняя) доверительная граница индивидуальных значений отклика. В соответствии с соотношениями (21), (22) использовались формулы: , s были взяты из таблицы 3. Через N (V) обозначена нижняя (верхняя) доверительная граница функции регрессии, через N инд (V инд) –нижняя (верхняя) доверительная граница индивидуальных значений отклика. В соответствии с соотношениями (21), (22) использовались формулы:
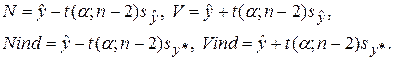
Графики доверительных границ, построенные по таблице 5, показаны на рис. 4.
Таблица 5. Расчеты доверительного интервала функции регрессии
| x
|
|
|
|
|
|
|
|
|
| 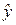
| 3, 34
| 4, 36
| 5, 38
| 6, 39
| 7, 41
| 8, 43
| 9, 44
| 10, 46
| 11, 48
| 
| 0, 78
| 0, 59
| 0, 43
| 0, 33
| 0, 35
| 0, 46
| 0, 63
| 0, 81
| 1, 01
| | N
| 1, 56
| 2, 99
| 4, 37
| 5, 62
| 6, 61
| 7, 36
| 7, 99
| 8, 58
| 9, 15
| | V
| 5, 13
| 5, 73
| 6, 38
| 7, 16
| 8, 21
| 9, 50
| 10, 89
| 12, 34
| 13, 80
| | sy*
| 1, 28
| 1, 18
| 1, 11
| 1, 08
| 1, 08
| 1, 12
| 1, 20
| 1, 31
| 1, 44
| | N ind
| 0, 38
| 1, 63
| 2, 81
| 3, 91
| 4, 92
| 5, 83
| 6, 67
| 7, 44
| 8, 16
| | V ind
| 6, 31
| 7, 09
| 7, 94
| 8, 88
| 9, 90
| 11, 02
| 12, 21
| 13, 48
| 14, 79
|
Для быстрого выполнения расчетов необходимо грамотно использовать абсолютные адреса ячеек Excel. Так, например, чтобы провести вычисления для двух значений доверительной вероятности (γ =0, 95 и γ =0, 9) достаточно:
- записать значение γ =0, 95 в ячейку листа Excel;
- выполнить расчеты, ссылаясь на эту ячейку с абсолютным адресом;
- изменить значение в ячейке с 0, 95 на 0, 9, чтобы получить результаты для γ =0, 9 (в результате автоматического пересчета по формулам).

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Весы настольные циферблатные Весы настольные циферблатные РН-10Ц13 (рис.3.1) выпускаются с наибольшими пределами взвешивания 2...
Хронометражно-табличная методика определения суточного расхода энергии студента Цель: познакомиться с хронометражно-табличным методом определения суточного расхода энергии...
ОЧАГОВЫЕ ТЕНИ В ЛЕГКОМ Очаговыми легочными инфильтратами проявляют себя различные по этиологии заболевания, в основе которых лежит бронхо-нодулярный процесс, который при рентгенологическом исследовании дает очагового характера тень, размерами не более 1 см в диаметре...
|
Характерные черты немецкой классической философии 1. Особое понимание роли философии в истории человечества, в развитии мировой культуры. Классические немецкие философы полагали, что философия призвана быть критической совестью культуры, «душой» культуры.
2. Исследовались не только человеческая...
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит...
Кран машиниста усл. № 394 – назначение и устройство Кран машиниста условный номер 394 предназначен для управления тормозами поезда...
|
|

 1, 02,
1, 02, 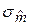 =0, 207 (см. таблицу 3); t (0, 05; 8)=2, 31 (с помощью функции СТЬЮДРАСПОБР). Подставив эти значения в формулу (18), получаем 95-процентный доверительный интервал для коэффициента m: 0, 538≤ m ≤ 1, 495.
=0, 207 (см. таблицу 3); t (0, 05; 8)=2, 31 (с помощью функции СТЬЮДРАСПОБР). Подставив эти значения в формулу (18), получаем 95-процентный доверительный интервал для коэффициента m: 0, 538≤ m ≤ 1, 495.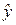 вычислялись по формуле (2),
вычислялись по формуле (2),  – по формуле (20), sy * – по формуле (23). Значения
– по формуле (20), sy * – по формуле (23). Значения 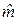 ,
, 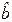 ,
, 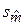 , s были взяты из таблицы 3. Через N (V) обозначена нижняя (верхняя) доверительная граница функции регрессии, через N инд (V инд) –нижняя (верхняя) доверительная граница индивидуальных значений отклика. В соответствии с соотношениями (21), (22) использовались формулы:
, s были взяты из таблицы 3. Через N (V) обозначена нижняя (верхняя) доверительная граница функции регрессии, через N инд (V инд) –нижняя (верхняя) доверительная граница индивидуальных значений отклика. В соответствии с соотношениями (21), (22) использовались формулы: