Оценивание значимости уравнения регрессии. Абсолютное значение выборочного коэффициента корреляции вычислим по формуле, следующей из (12а):Абсолютное значение выборочного коэффициента корреляции вычислим по формуле, следующей из (12а): Значения остаточной и регрессионной суммы получим из таблицы 3: Qe =8, 39, QR =25, 21. Так как QR > > Qe, то, скорее всего, уравнение регрессии значимо. Полную сумму квадратов вычислим по формуле (11): Q =33, 60. Смысл этих сумм был разъяснен в §1.5. Проверим гипотезу о незначимости уравнения регрессии по критерию Фишера. Из таблицы 3: F =24, 03. Квантиль F -распределения вычислим с помощью функции FРАСПОБР: f (0, 05; 1; 8)=5, 32. Таким образом, неравенство (14) выполнено, и уравнение значимо. Проверим гипотезу H о равенстве нулю коэффициента регрессии. Из таблицы 3: 3. Задание* на самостоятельную работу Исследуется зависимость доли расходов на продовольственные товары в общих расходах (Y) от средней дневной заработной платы одного работающего (X) в семи территориях Уральского региона по данным, представленным в таблице 4. Провести анализ зависимости Y (X) по аналогии с §2.
Таблица 4. Зависимость доли расходов от средней заработной платы
Практическая работа №2. Интервальное оценивание
|
. Значение R 2 берем из таблицы 3 результатов функции ЛИНЕЙН: R 2=0, 750, | r |=0, 866. Следовательно, связь между Y и X достаточно тесная.
1, 02,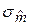 
=0, 207. По формуле (15в) определяем: Т =4, 90. Квантиль распределения Стьюдента вычислим с помощью функции СТЬЮДРАСПОБР: t (0, 05; 8)=2, 31. Получили, что неравенство (16) выполнено. Следовательно, гипотезу H следует отклонить, и коэффициент регрессиизначим.
