Интервальное оценивание функции регрессииПод функцией регрессии (см. §1.1) понимается f (x)≡ MxY – условное математическое ожидание отклика Y при заданном значении x фактора. Из несмещенности оценок
Можно доказать (см., например, [5]), что для выборочного среднего квадратичного отклонения
а центрированная и нормированная статистика
распределена по Стьюденту с числом степеней свободы n -2. Отсюда следует, что с вероятностью γ =1-a выполняется соотношение:
и доверительный интервал MxY надежности γ определяется неравенством:
Из соотношений (20), (21), в частности, следует, что величина доверительного интервала функции регрессии зависит от значения объясняющей переменной х: чем больше отклонение х от среднего значения
|
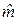и 
и 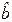соотношения (2) следует:
.
справедлива формула:
, (20)
,
(21)
, тем шире доверительный интервал, и, соответственно, меньше точность оценивания.
