Асимптоты плоской кривой
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой. Для кривой, которая является графиком функции
Прямая х = а является вертикальной асимптотой графика функции
если значение х = а является точкой бесконечного разрыва функции или границей ее области определения.
Прямая
Если хотя бы один из этих пределов не существует и равен бесконечности, то кривая
При вычислении, пределы (1) могут быть различными при х®+¥ и при х®–¥.
Пример 1. Найти асимптоты графика функции
Решение. Область определения функции: х ¹ 3, поэтому х = 3 является точкой разрыва функции. Вычисляем Наклонные (горизонтальные) асимптоты ищем уравнением
Таким образом, график функции Ответ: х = 3, y = 5.
Пример 2. Найти асимптоты графика функции
Решение. Область определения функции: х ¹ 1 Þ х = 1 – точка разрыва графика. Так как
Þ y = 3x + 3 – наклонная асимптота. Ответ: х = 1, y = 3x + 3.
Пример 3. Найти асимптоты графика функции
Решение. Область определения функции: х > 0. На границе области определения возможна вертикальная асимптота. Вычисляем Наклонные (горизонтальные) асимптоты: где
Þ наклонных асимптот нет. Ответ: х = 0 при х ® + 0.
Пример 4. Найти асимптоты графика функции Решение. Область определения функции: х ¹ 1. Т.к. Наклонные асимптоты:
Þ при х ® +¥ наклонных (горизонтальных) асимптот нет.
Þ y = 0 – горизонтальная асимптота только при х ® -¥.
Ответ: х = 1, y = 0 (при х ® -¥).
Дополнительные упражнения.
Найти уравнения асимптот графиков следующих функций.
Ответы.
|

 , различают вертикальные, наклонные и горизонтальные асимптоты.
, различают вертикальные, наклонные и горизонтальные асимптоты.
 или
или  , т.е.
, т.е. является наклонной (при k = 0 горизонтальной) асимптотой графика функции
является наклонной (при k = 0 горизонтальной) асимптотой графика функции  , и
, и  . (1)
. (1) .
.
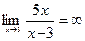 и заключаем, что прямая х = 3 является вертикальной асимптотой графика.
и заключаем, что прямая х = 3 является вертикальной асимптотой графика.
 =
=  ,
,
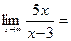
 =
= 
 .
.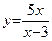 имеет две асимптоты: вертикальную х = 3 и горизонтальную y = 5 при х®±¥.
имеет две асимптоты: вертикальную х = 3 и горизонтальную y = 5 при х®±¥. .
.
 ¥, то прямая х = 1 является вертикальной асимптотой. Наклонные (горизонтальные) асимптоты:
¥, то прямая х = 1 является вертикальной асимптотой. Наклонные (горизонтальные) асимптоты: , где
, где 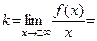
 3,
3,
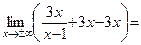

 3
3 .
.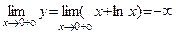 и заключаем, что прямая х = 0 является правосторонней вертикальной асимптотой.
и заключаем, что прямая х = 0 является правосторонней вертикальной асимптотой. ,
,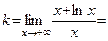

 = 1,
= 1,

 .
.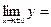

 , то прямая х = 1 является вертикальной асимптотой графика (двухсторонней).
, то прямая х = 1 является вертикальной асимптотой графика (двухсторонней). Þ
Þ  .
.






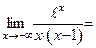 0,
0,
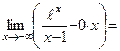 0
0 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
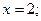
 ;
;
 ,
,  ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
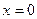 (при
(при  ),
),  ;
;



