Раскрытие неопределенностей или
Вычислить следующие пределы, применяя правило Лопиталя.
Пример 1.
Решение. Здесь
Поэтому данный предел содержит неопределенность Так как функции f(x) и
Получилось, что предел отношения производных существует и равен числу Ответ:
Пример 2.
Решение.
Пояснение к символу “V”: после того, как обнаружена неопределенность
В конце концов предел отношения третьих производных вычислился и равен числу
Таким образом, правило Лопиталя применено три раза, в результат получено значение искомого предела и этот факт отражается в записях с использованием символа “V”. При этом важно понимать, что если бы получилось так, что предел отношения оказался несуществующим, то это бы не означало, что не существуют и предыдущие пределы (то есть переходы “” в этом случае делать нельзя). Это только лишь означало бы, что данный предел не может быть вычислен по правилу Лопиталя.
Ответ:
Пример 3.
Решение.
Ответ: 2.
Пример 4.
Решение.
Здесь работа по правилу Лопиталя значительно упростилась применением теоремы о пределе произведения, с помощью которой была отделена функция Ответ:
Пример 5.
Решение.
Ответ:
Пример 6.
Решение.
Это значит, что не выполняется одно из условий правила Лопиталя – условие существования предела отношения производных двух функций. Поэтому предел отношения этих двух функций не может быть вычислен по правилу Лопиталя, хотя может существовать и быть вычислен иными приемами. Действительно, Таким образом, работая с пределом по правилу Лопиталя, нельзя быть уверенным в его успешном вычислении до тех пор, пока не получится значение (конечное или бесконечное) предела отношения производных некоторого порядка. Только в этом случае становятся справедливыми все равенства в цепочке
|


 Þ
Þ 
 Þ
Þ 
 .
. дифференцируемы в окрестности точки х = –1, то попробуем вычислить предел отношения их производных:
дифференцируемы в окрестности точки х = –1, то попробуем вычислить предел отношения их производных:
 =
=  =
=  =
=  .
. также существует и равен числу
также существует и равен числу  .
. .
.
 V
V 
 V V
V V 

 .
. . Теперь в соответствии с правилом Лопиталя заключаем, что все пределы отношений предыдущих производных и самих функций существует и равен
. Теперь в соответствии с правилом Лопиталя заключаем, что все пределы отношений предыдущих производных и самих функций существует и равен 
 .
. .
.

 =
= 
 =
= 


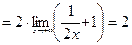 .
. .
.
 V
V 
 =
=  =
=  =
= 
 V
V 

 , не участвующая в создании неопределенности.
, не участвующая в создании неопределенности. .
. .
.
 V
V 
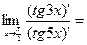

 V V
V V 






 .
. V
V 



 – не существует.
– не существует.



 ¼
¼ 



