ВВЕДЕНИЕ 4 страница. а) по определению положительны;
а) по определению положительны; б) отрицательны; в) могут быть положительными или отрицательными, от чего при этом зависит знак?
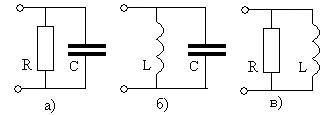
8. Какое явление в RLC цепи называется резонансом, в чем оно проявляется? 9. Что представляет собой треугольник сопротивлений? В каком случае говорят об индуктивном или емкостном характере сопротивления цепи? Каким характером сопротивления обладают цепи с треугольниками сопротивлений, приведенными на рис.4.12а, б? 10. Чему равна средняя мощность в электрической цепи, векторная диаграмма которой показана на рис.4.13?
Рис. 4.12 Рис. 4.13 ЗАДАЧИ
4.1. (2 балла). Определите активную R, реактивную x составляющие и полное сопротивление Z ветви между точками a и b цепи (рис.4.14) при следующих данных:
R=(300+100G + 0, 5(N-20)2) Ом, L=(800-10(-1)N+GN) мкГн, C= (100 – 0, 1(-1)N+GN) нФ. Какой характер имеет сопротивление цепи?
Рис. 4.14
Значение Z (Ом) внесите в АКОС-1 со знаком минус (условно) в случае емкостного характера сопротивления, со знаком плюс - в случае индуктивного или активного характера сопротивления. 4.2. (2 балла). Присоедините цепь (рис.4.14) мысленно к источнику гармонического тока с амплитудой Jm=1A по схеме рис. 4.15. Определите при данных задачи 4.1: а) амплитуды напряжений на сопротивлении, индуктивности и емкости (UmR, UmL и UmC соответственно); б) амплитуду напряжения Um между точками a и b. Значение UmL в вольтах внесите в АКОС. 4.3. (2 балла). Присоедините цепь (рис.4.14) к источнику гармонической ЭДС с амплитудой Em=200 В по схеме, изображенной на рис.4.16. Найдите: а) амплитуду тока Im, возникающего под действием приложенной к цепи ЭДС, при данных из задачи 4.1; б) начальную фазу тока в) среднюю мощность P, потребляемую цепью, двумя способами: - по известным значениям Um=Em, Im и разности фаз между напряжением или ЭДС и током - по известному току Im и активному сопротивлению R.
4.4. (2 балла). Рассмотрите схему (рис.4.17) с коммутирующими ключами k0, k1,... ks, изображенными на чертеже. Установите ключ k0 в положение 0, если ваш номер четный или в положение 1, если номер - нечетный. Остальные ключи установите в положения, соответствующие числу N, записанному в двоичной системе исчисления (N2), как показано на рис.4.18. В верхней строке рис.4.18 обозначены пять ключей из схемы (рис.4.17), в нижней записан порядковый номер студента N в двоичной форме (в качестве примера N=13).
Ключ k1 устанавливается в положение " 1", поскольку под ним оказалась цифра 1, ключ k2 - в положение " 0" и т.д.
Рис. 4.18
Зарисуйте получившуюся таким путем при Вашем N схему без изображения ключей, исключив из нее также элементы, оказавшиеся закороченными. Примите
R=(1+0, 1G) кОм, L=(10+N) мГн, C=(1+N) нФ. Em=(900-10N) мВ, Im=(350+(-1)N 4N) мкА,
Определите: а) сопротивление Z соединения RLC между точками a, b (рис.4.17); б) амплитуду тока Im через соединение; в) амплитуду напряжения на соединении Um; г) начальную фазу напряжения д) начальную фазу тока е) разность фаз между напряжением и током
Вычислите значение Ia=Imcos 4.5. (2 балла). Замените величину C в задаче 4.1 другим ее возможным значением C1 так, чтобы величина Z осталась прежней. Получите формулу и определите величину C1 при данных задачи 4.1. Изменится ли при замене C на C1 характер сопротивления Z цепи рис.4.14? Значение емкости C1 в пикофарадах, вычисленное при данных задачи 4.1, внесите для проверки в АКОС. 4.6. (2 балла). Определите значение индуктивности L, которую необходимо включить последовательно с осветительной лампой (сопротивление Rл, рис.4.19) для того, чтобы действующее значение напряжения на ней было равно Uл=(70+2N)В при амплитудах напряжения питания Um=(180+N) В и тока в цепи Im=(0, 8+0, 1G) А на частоте F=50 Гц. Определите мощность P=P1, потребляемую цепью от источника.
Рис. 4.19
Решите поставленную задачу, заменив индуктивность L активным сопротивлением R. Определите мощность P=P2, отбираемую от источника во втором случае, сопоставьте ее со значением P1.Вычислите для проверки величину
в миллигенри и внесите ее в АКОС.
ДЛЯ ПЫТЛИВЫХ
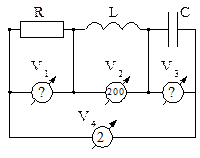
4.1. Какие из осциллограмм на рис.4.20 (1, 2, 3) относятся к напряжениям на R, L, C? Сопротивление какого характера имеет цепь, к которой относятся осциллограммы? 4.2. Чему равны показания первого и третьего вольтметров в цепи рис.4.21 при резонансе, если известны показания второго и четвертого вольтметров 200В и 2В соответственно?
Рис. 4.20 Рис. 4.21
ОСНОВНЫЕ ФОРМУЛЫ
[2, с. 87 - 106].
ТЕМА 5. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ R, L и C
КОНТРОЛЬНЫЕ ВОПРОСЫ
2. Какими данными цепи (рис.5.1) определяется угол сдвига фаз Рис.5.1 нию? Какова расчетная формула? В каких случаях
3. При каком условии угол сдвига фаз 4. Чему равны проводимости двухполюсных соединений, изображенных на рис.5.2, а, б, в? Какой характер (индуктивный или емкостный) имеют про-водимости каждого из этих двухполюсников? Рис.5.2
6. Чему равна средняя мощность тока в цепи (рис.5.1)? По каким формулам ее можно определить при условиях: а) когда известны амплитуды (или действующие значения) напряжения и тока в цепи и угол сдвига фаз между ними? б) когда известно напряжение в) при известном сопротивлении R и токе 7. Какой вид имеют треугольники проводимостей цепи, изображенной на рис.5.1, и ее " укороченных" вариантов на рис.5.2?
ЗАДАЧИ
5.1. (2 балла). Найдите полную проводимость
R=(100 + N*G) Ом, L= (200 + (-1) N4N) мкГн, C= (300 + 20N+30G) нФ.
Частота источника питания цепи Площадь сах в квадрате) построенного Рис.5.4 Вами треугольника проводи- мостей и внесите величину 5.2. (2 балла). Присоедините цепь (рис.5.4) к источнику
Рис. 5.5 и векторов токов в ветвях
Дополните чертеж по правилам геометрического сложения вектором общего (суммарного) тока ветвей
Проверьте измерения вычислением и занесите величину 5.3. (2 балла). Измените по сравнению с задачей 5.1 частоту источника питания цепи (рис.5.47), установив ее равной 5.4. (2 балла). Установите переключатели в цепи (рис.5.6) в положения, соответствующие двоичной записи вашего номера N, подобно тому, как это делалось в теме 4. Зарисуйте полученную таким образом схему, упростите ее, объединив одноименные элементы, удалите отключенные ветви.
Рис. 5.6
Воспользуйтесь следующими параметрами элементов цепи:
R= (300 + 0, 1NG) Ом, L= (
C= (300 + (-1) N(N + G)) нФ, ω = 2π 105 рад/с,
Найдите амплитуду тока
L= [300+(-1)N+G 2 (N +G)] мкГн,
Рис. 5.7 Найденное значение емкости С в нанофарадах внесите для проверки в АКОС.
Емкость конденсатора Рис. 5.8 примите равной
C=[ 7 + (-1)N 0, 01 N G ] (13 - G) нФ,
частоту источника ДЛЯ ПЫТЛИВЫХ
5.1. Три вектора 1, 2, 3 на диаграмме (рис.5.9) соответствуют трем токам через элементы R, L и C в их параллель-
ческой частоте
ОСНОВНЫЕ ФОРМУЛЫ
ТЕМА 6. МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД
КОНТРОЛЬНЫЕ ВОПРОСЫ
Запишите, чему равна комплексная амплитуда в экспоненциальной форме для гармонического напряжения, Рис. 6.1 представленного равенством
2. Комплексная амплитуда гармонического напряжения в алгебраической форме равна 3. По каким формулам осуществляется переход от показательной формы записи комплексного числа к алгебраической и наоборот? Чему равны вещественная и мнимая части комплексного числа в показательной форме? Чему равны модуль и аргумент комплексного числа в алгебраической форме? 4. Чему равна комплексная амплитуда
6. Чему равны модуль 7. Чему равны модули и аргументы: Рис. 6.2 а) вещественного числа б) мнимых чисел в) комплексной величины г) числа
Справка: arctg(3/5)= 0, 54 и arctg(5/3)= 1, 03. 8. Изобразите на комплексной плоскости векторы двух гармонических колебаний, заданных комплексными амплитудами: а) б)
ЗАДАЧИ
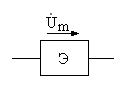
6.1. (1 балл). Гармоническое напряжение на некотором элементе цепи Э (рис.6.3) определяется равенством:
где Um= (800 + (-1)N 10 N) В, λ = (6 G + 0, 1 N)0. Приведите это выражение к каноническому виду
укажите, чему равна комплексная амплитуда Рис. 6.3 ки. 6.2. (2 балла). Комплексная амплитуда напряжения на элементе цепи определяется выражением
Найдите при этих значениях 6.3. (3 балла). Напряжения на двух последовательно соединенных элементах цепи (рис.6.4) заданы их комплексными амплитудами в разной форме записи (алгебраической и показательной):
|

 7. Каким выражением определяется угол сдвига фаз
7. Каким выражением определяется угол сдвига фаз 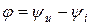 между напряжением и током в цепи с известными значениями X и R? В каких пределах заключены возможные значения
между напряжением и током в цепи с известными значениями X и R? В каких пределах заключены возможные значения 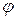 для RLC, RC, RL, LC цепей?
для RLC, RC, RL, LC цепей?
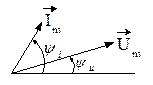
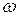 = 106 рад/с,
= 106 рад/с,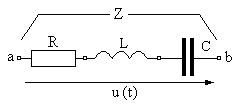
 , полагая начальную фазу ЭДС источника равной
, полагая начальную фазу ЭДС источника равной 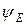 =0;
=0; Напишите выражение для тока i(t) с учетом найденных значений Im и
Напишите выражение для тока i(t) с учетом найденных значений Im и 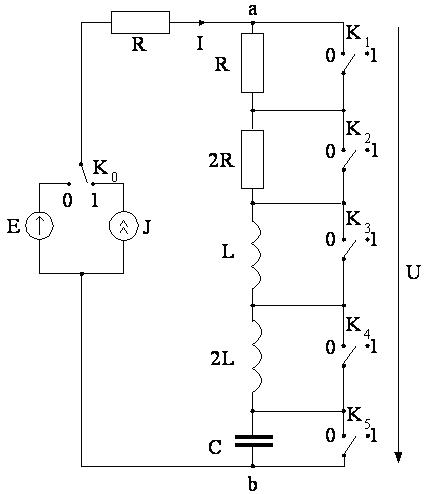 Рис. 4.17
Рис. 4.17 =(-1)G (60-2N) град,
=(-1)G (60-2N) град, ;
;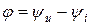 .
.







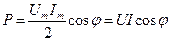
 ЛИТЕРАТУРА
ЛИТЕРАТУРА 1. Чему равна проводимость элементов R, L, C и модуль полной проводимости Y их параллельного соединения (рис.5.1)?
1. Чему равна проводимость элементов R, L, C и модуль полной проводимости Y их параллельного соединения (рис.5.1)? тока по отношению к напряже-
тока по отношению к напряже- и
и 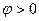 в цепи рис.5.4?
в цепи рис.5.4? и током
и током 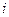 в цепи (рис.5.1) равен нулю, как называется явление, наблюдаемое в параллельной RLC - цепи при этом условии? Чему равна амплитуда тока
в цепи (рис.5.1) равен нулю, как называется явление, наблюдаемое в параллельной RLC - цепи при этом условии? Чему равна амплитуда тока  при параллельном резонансе? Равны ли при этом нулю токи через L и C в отдельности?
при параллельном резонансе? Равны ли при этом нулю токи через L и C в отдельности? 5. К каким из рассмотренных выше элементов цепей R, L и C или их параллельным соединениям (рис.5.1 и 5.2) относятся векторные диаграммы, приведенные на рис.5.3, а-д?
5. К каким из рассмотренных выше элементов цепей R, L и C или их параллельным соединениям (рис.5.1 и 5.2) относятся векторные диаграммы, приведенные на рис.5.3, а-д? Рис.5.3
Рис.5.3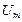 и сопротивление R?
и сопротивление R?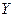 цепи (рис.5.4) и ее активную
цепи (рис.5.4) и ее активную  и реактивную
и реактивную 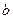 составляющие в миллисимменсах при следующих данных:
составляющие в миллисимменсах при следующих данных: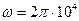 рад/с. Определите характер проводимости цепи (индуктивная, емкостная). Постройте треугольник проводимостей. Вычислите с проверочной целью
рад/с. Определите характер проводимости цепи (индуктивная, емкостная). Постройте треугольник проводимостей. Вычислите с проверочной целью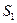 (в микросиммен-
(в микросиммен- гармонической ЭДС с амплитудой Em = 200 В (рис.5.5), создающему напряжение
гармонической ЭДС с амплитудой Em = 200 В (рис.5.5), создающему напряжение 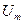 между выводами цепи. Постройте при параметрах цепи из задачи 5.1 векторную диаграмму с отображением на ней вектора напряжения
между выводами цепи. Постройте при параметрах цепи из задачи 5.1 векторную диаграмму с отображением на ней вектора напряжения 
 ,
, 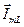 ,
, 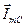 с учетом их длины и углового положения. Примите при построениях начальную фазу напряжения
с учетом их длины и углового положения. Примите при построениях начальную фазу напряжения 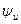 равной нулю.
равной нулю. , измерьте его длину и определите с учетом масштаба диаграммы величину его амплитуды
, измерьте его длину и определите с учетом масштаба диаграммы величину его амплитуды 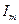 . Измерьте транспортиром угол
. Измерьте транспортиром угол 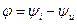 .
.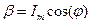 в миллиамперах в АКОС со знаком минус, если ток в рассматриваемой цепи о т с т а е т по фазе от напряжения и со знаком плюс в противоположном случае.
в миллиамперах в АКОС со знаком минус, если ток в рассматриваемой цепи о т с т а е т по фазе от напряжения и со знаком плюс в противоположном случае.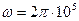 рад/с. Постройте повторно, применительно к новому значению частоты, треугольник проводимостей и определите характер (емкостный или индуктивный) проводимости цепи. Внесите в АКОС площадь
рад/с. Постройте повторно, применительно к новому значению частоты, треугольник проводимостей и определите характер (емкостный или индуктивный) проводимости цепи. Внесите в АКОС площадь  треугольника проводимостей в миллисимменсах в квадрате со знаком минус, если проводимость емкостная, или без него в противном случае.
треугольника проводимостей в миллисимменсах в квадрате со знаком минус, если проводимость емкостная, или без него в противном случае.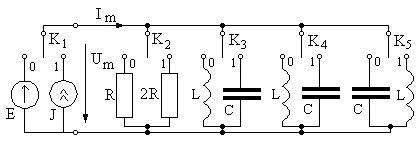
 + 0, 03NG) мкГн,
+ 0, 03NG) мкГн,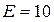 В,
В, 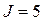 А.
А.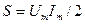 и внесите ее значение в вольт-амперах в АКОС.
и внесите ее значение в вольт-амперах в АКОС. 5.5. (2 балла). Определите, какую емкость C в цепи (рис.5.7) следует включить параллельно индуктивности L для того, чтобы ток Im при заданной амплитуде ЭДС Em источника был минимальным. Примите:
5.5. (2 балла). Определите, какую емкость C в цепи (рис.5.7) следует включить параллельно индуктивности L для того, чтобы ток Im при заданной амплитуде ЭДС Em источника был минимальным. Примите: 5.6. (2 балла). Какую следует выбрать индуктивность L в цепи (рис.5.8), чтобы отключение ее или подключение параллельно емкости C посредством ключа K не сказывалось на амплитуде тока источника Im. Внесите величину L в миллигенри в АКОС для проверки.
5.6. (2 балла). Какую следует выбрать индуктивность L в цепи (рис.5.8), чтобы отключение ее или подключение параллельно емкости C посредством ключа K не сказывалось на амплитуде тока источника Im. Внесите величину L в миллигенри в АКОС для проверки. рад/с.
рад/с.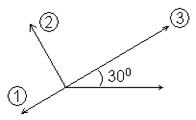 ном соединении (рис.5.5). Какие векторы соответствуют токам
ном соединении (рис.5.5). Какие векторы соответствуют токам 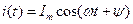 при цикли- Рис. 5.9
при цикли- Рис. 5.9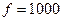 Гц.
Гц.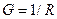
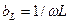



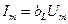
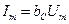
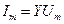


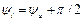

 1. Чему равна комплексная амплитуда
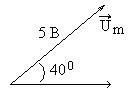
1. Чему равна комплексная амплитуда 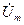 гармонического напряжения
гармонического напряжения  , представленного вектором на рис.6.1? Представьте ее в трех формах записи (показательной, тригонометрической, алгебраической).
, представленного вектором на рис.6.1? Представьте ее в трех формах записи (показательной, тригонометрической, алгебраической). В.
В.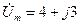 В и частота
В и частота  Гц. Представьте колебание в виде тригонометрической функции времени. Справка: arctg(0, 75)= 36, 90.
Гц. Представьте колебание в виде тригонометрической функции времени. Справка: arctg(0, 75)= 36, 90. и
и  и векторами на рис.6.2.? Чему равна амплитуда
и векторами на рис.6.2.? Чему равна амплитуда  результирующего колебания? Найдите их аналитически, исходя из
результирующего колебания? Найдите их аналитически, исходя из 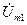 и
и  . Как их можно найти геометрическим путем, исходя из рис.6.2?
. Как их можно найти геометрическим путем, исходя из рис.6.2?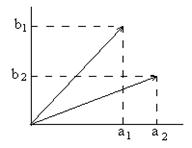
 5. Чему равны модуль
5. Чему равны модуль 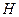 и аргумент
и аргумент 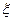 произведения
произведения 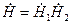 двух комплексных величин
двух комплексных величин  и
и 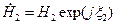 ?
? двух комплексных чисел
двух комплексных чисел 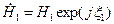 и
и 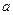 ;
; и
и 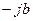 ;
;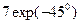 ;
;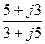 ?
?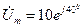 В и
В и  А;
А;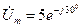 В и
В и  А;
А; в)
в)  В и
В и  А;
А;

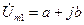 и занесите мнимую часть
и занесите мнимую часть в вольтах в АКОС для провер-
в вольтах в АКОС для провер- где
где 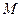 , равную
, равную  , где
, где 


