ВВЕДЕНИЕ 9 страница
ЗАДАЧИ
21.1 (1 балл). Составьте дифференциальные уравнения для тока i(t) или напряжения на конденсаторе uC(t) в выделенных жирными линиями колебательных контурах (рис.21.1 или рис. 21.2). Определите при нижеследующих данных: L = (100 + (-1)N× 2 N + 8 G) мГн, C = (6000 - (-1) N× 50 N + 100 G) пФ, R = (7800 + 50 N - 18 G) Ом, какого рода процесс протекает в свободном от источников
контуре путем анализа корней его характеристического уравнения. В зависимости от процесса примите следующие значения индекса J: апериодический - J=12, критический - J=1, колебательный - J=-5.
Изобразите в тетради качественно (без вычислений), какой вид имеет функция i(t) или uC(t) при заданных значениях L, C и R. Обратитесь к схемам: - рис.21.1 - для студентов с четными значениями N, - рис.21.2 - для студентов с нечетными значениями N. Определите, исходя из законов коммутации, начальные условия uC(0) в вольтах и iL(0) в амперах для своей цепи при
Е = (400 + (-1) N× 5 N + 10 G) B, R1 = 10 + N Ом, R2 = 50 - G Ом.
Вычислите с проверочной целью величину
B=J [uC(0)+iL(0)]
и внесите ее в АКОС.
Рис.21.1
Рис.21.2
21.2 (2 балла). Примите для цепи рис.21.1 значение сопротивления потерь равным R = (12 + 2 N + (-1) N× G) Ом при L и C, заданных в задаче 21.1. Какого рода процесс (апериодический, колебательный) будет наблюдаться в контуре (рис.21.1) после замыкания ключа К? Напишите выражение для тока в контуре в рассматриваемом случае, подставьте в него все необходимые численные данные, исходя из заданных Вам параметров контура и ЭДС источника Е (задача 21.1). Рассчитайте и постройте по точкам кривую i(t). Определите значение тока i(t1) в амперах в момент времени t = (100 + (-1) N× 2 N+2 G) мкс и внесите величину i(t1)× 104 в АКОС для проверки. Нанесите значения корней характеристических уравнений, полученных Вами в задачах 21.1 и 21.2, в виде точек на комплексную плоскость (рис.21.3). В какой полуплоскости и на каких полуосях расположились точки? Свяжите их расположение с характером протекающих в цепи свободных процессов. 21.3. (2 балла). Рассчитайте и постройте в масштабе кривую изменения напряжения на емкости uC(t) контура (рис.21.1) по приближенной формуле U(t)=UC0e-at cos(w0t), справедливой для контуров с пренебрежимо малым значением коэффициента затухания a по сравнению с резонансной частотой контура w0. Для исходных данных из предыдущих задач определите: а) период затухающих свободных колебаний в контуре T = 2p/w0 секунд; б) постоянную времени затухания амплитуды колебаний t= 1/a с размерностью единица, деленная на секунду; в) логарифмический декремент затухания колебательного процесса q. Вычислите величину, равную D = (q× t× TC) 1010 и внесите ее в АКОС для проверки. 21.4. (2 балла). Найдите, какое число n полных колебаний напряжения на конденсаторе совершается в колебательном контуре (рис.21.1) при данных L и C из задачи 21.1 и R из задачи 21.2 от начала процесса до его практически полного затухания, когда амплитуда напряжения упадет не менее чем в 10× G× N раз. Ответьте на вопрос – число n с повышением добротности контура Q: - увеличивается (J=1), - уменьшается (J=-1)? Вычислите величину, равную H = J× n и внесите ее для проверки в АКОС. 21.5. (2 балла). Вычислите и постройте кривую изменения напряжения на конденсаторе uC(t) при включении источника ЭДС Е в контур (рис.21.4) посредством ключа К. Определите, какого уровня достигает напряжение на конденсаторе в максимуме и в какой момент времени W =(10 + (-1)N × G + 5 N) крад/с, a= (120 - (-1) N × 2 N) 1/с, E =(1500 + (-1) N × 20 N + 10 G) В.
Объясните физически, за счет чего образуется выброс напряжения на конденсаторе, существенно превышающий напряжение источника Е. 21.6. (2 балла). Какой вид имеет напряжение на конденсаторе UС(t) при включении в нулевой момент времени гармонической ЭДС e(t)=Emcos(wt) в контур рис.21.5 (w совпадает с резонансной частотой контура). Напишите выражение и изобразите графически огибающую процесса нарастания амплитуды напряжения на емкости в виде функции времени при следующих данных:
Q = (120 + (-1)N× N + 2 G), w = (500 + 10 N G + (-1)N× 250) рад/с.
Рис.21.4 Рис. 21.5
Определите время t, по истечении которого амплитуда достигнет половины установившегося значения и внесите его в микросекундах в АКОС.
Тема 22 ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
КОНТРОЛЬНЫЕ ВОПРОСЫ
22.1. Запишите прямое и обратное преобразование Лапласа. 22.2. Как с помощью таблиц проводится преобразование Лапласа? В каком виде должно быть представлено изображение? Приведите примеры. 22.3. Сформулируйте законы Ома и Кирхгофа в операторной форме. Какими методами можно составить полную систему операторных уравнений? Приведите примеры для цепи, показанной на рис. 20.1а. 22.4. Как учитываются ненулевые начальные условия для индуктивности и емкости? Сформируйте эквивалентную схему замещения для цепи на рис. 20.1б. Запишите для нее полную систему операторных уравнений. 22.5. Как полином представляется в виде произведения простых сомножителей? Каким образом отношение двух полиномов представляется в виде суммы простых дробей? 22.6. Как связаны между собой операторный и комплексный коэффициенты передачи четырехполюсника?
ЗАДАЧИ
22.1 (3 балла) В цепи рис.22.1 при разомкнутом ключе К определите операторное выражение требуемой характеристики: входного сопротивления Z(p) при четных N или входной проводимости Y(p) при нечетных N. Для расчетов примите: R1= (2 + (-1)N× G/10) кОм, R2= (2 + N/10) кОм, R3= (5 - N/10) кОм, R4= (1, 5 - (-1) N× G/15) кОм, R5(3 + (-1) N× N/20) кОм, RH= 3 кОм, C= (60 + 2 N) нФ, L = (1, 5 G) Гн.
Рис.22.1
Представьте полученное операторное выражение F(p) в виде
Значения параметра А в омах при четных N или в микросименсах при нечетных N введите в АКОС для проверки. 22.2 (3 балла) В условиях задачи 22.1 при замкнутом ключе К определите коэффициент передачи цепи по напряжению Ku(p)=U2(p)/U1(p) для четных N или коэффициент передачи цепи по току Ki(p)=I2(p)/I1(p) для нечетных N. Представьте полученное выражение в форме, указанной в задаче 22.1. Вычислите значения 1000A и 1000 (a0/b0) и внесите их в АКОС. 22.3 (2 балла) На вход цепи рис.22.1 с параметрами из задачи 22.1 при замкнутом ключе К в момент времени t=0 подключается идеальный источник напряжения с ЭДС Е0=(G+10) В для четных N или идеальный источник тока с током I0 = (G+5) мА для нечетных N. Операторным методом определите зависимость от времени выходного напряжения U2(t) для четных N или тока I2(t) для нечетных N. Значение U2(t) в милливольтах или I2(t) в микроамперах при t = (200 + (-1) N× 4 N) мкс введите для проверки в АКОС.
Справка:
Задача 22.4 (2 балла) Определите переходную характеристику h(t) цепи рис.22.1 при отключенной нагрузке Rн для четных N или подключенной нагрузке для нечетных N. Значение 10000 h(t) при t из задачи 22.3 занесите в АКОС. Задача 22.5 (2 балла) Определите импульсную характеристику g(t) цепи рис.22.1 при подключенной нагрузке Rн для четных N или отключенной нагрузке для нечетных N. Значение g(t) при размерности единица, деленная на секунду, в момент времени t из задачи 22.3 введите в АКОС.
Тема 23 РАСЧЕТ РЕАКЦИИ ЦЕПИ НА СЛОЖНЫЙ ВХОДНОЙ СИГНАЛ МЕТОДОМ ИНТЕГРАЛА ДЮАМЕЛЯ КОНТРОЛЬНЫЕ ВОПРОСЫ 23.1. Запишите интеграл Дюамеля. Как с его помощью определяется реакция цепи на сложное входное воздействие? 23.2. Дайте определение переходной и импульсной характеристик. Каков их физический смысл? 23.3. Как связаны между собой переходная и импульсная характеристики цепи? Как они связаны с операторным коэффициентом передачи? 23.4. Как определяются переходная и импульсная характеристики цепи операторным методом? Приведите пример.
ЗАДАЧИ
23.1 (4 балла) Методом интеграла Дюамеля для цепи рис.22.1 (рассматривавшейся в предыдущей теме 22) при разомкнутом ключе К для четных N и замкнутом - для нечетных N определите переходную h(t) и импульсную g(t) характеристики, а также реакцию Uвых(t) на входной сигнал Uвх(t) вида:
где Umax=30 + (-1)N× N/2 В, a = 104× (12 + G) 1/с. Постройте графики зависмостей h(t), g(t) и Uвых(t) в интервале времени от нуля до 100 мкс, проанализируйте их с физической точки зрения. Вычислите безразмерную величину 1000 h(t=0) и введите ее в АКОС-1. Определите выходное напряжение Uвых(t) в милливольтах при t = (50 - N/2) мкс и внесите его для проверки в АКОС. 23.2 (1 балл) Определите, имеется ли скачкообразное изменение выходного сигнала Uвых(t) в момент времени t=0. Объясните причину возникновения скачка и выберите индекс ответа J1: а) из-за того, что переходная характеристика скачкообразно изменяется при t=0 - J1=1; б) из-за того, что переходная характеристика стремится к конечному пределу при увеличении t - J1=2; в) из-за того, что импульсная характеристика отрицательна при положительных t - J1=3. Вычислите произведение J1× Uвых(t=0) в милливольтах и введите его в АКОС. 23.3 (2 балла) Определите значение параметра затухания (a) входного сигнала, при котором форма выходного сигнала Uвых(t) с точностью до постоянного множителя совпадает с формой входного сигнала Uвх(t). Объясните причину, по которой форма переходного процесса на выходе цепи может совпадать с формой входного воздействия, и выберите индекс ответа J2: а) в цепи отсутствует свободная составляющая переходного процесса - J2=1; б) в цепи отсутствует принужденная составляющая переходного процесса - J2=2; в) форма свободной составляющей переходного процесса совпадает с формой принужденной составляющей - J2=3. Значение (J2× a) с размерностью единица, деленная на секунду, введите в АКОС. Задача 23.4 (5 баллов) На вход цепи рис.22.1 поступает импульсный сигнал, показанный на рис.23.1,
Рис.23.1
Примите T = (60 + (-1)N× N) мкс, а значения Umax, параметров цепи и положение ключа К возьмите из задачи 23.1. Методом интеграла Дюамеля определите выходной сигнал Uвых(t). Вычислите два значения выходного сигнала Uвых и Uвых в милливольтах в моменты времени t1 = T/2 и t2 = 1, 2 T соответственно, и введите их в АКОС-1 для проверки.
|

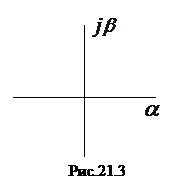


 это имеет место. Найдите произведение G =
это имеет место. Найдите произведение G = 



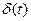 - функция Дирака.
- функция Дирака.





