ВВЕДЕНИЕ 3 страница. При осциллографических измерениях удобно иметь в виду следующее очевидное равенство (пропорцию) для в радианах:
При осциллографических измерениях удобно иметь в виду следующее очевидное равенство (пропорцию) для
отсюда
а знак определять по направлению смещения графика колебания относительно опорного сигнала.
По определению (3.1) гармоническое колебание - это вечный процесс, простирающийся справа и слева по оси времени до бесконечности. Формула (3.1) справедлива для любых значений времени t без ограничения. Реальный процесс имеет начало и конец. В интервале времени от установления колебаний до выключения источника можно, однако, в большинстве случаев считать процесс с достаточной для практики точностью гармоническим.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое колебание называется гармоническим, какими функциями времени оно выражается? 2. Какие величины в выражении носят названия - мгновенное значение колебания, амплитуда колебания, начальная фаза, полная фаза, угловая частота? 3. Выразите угловую частоту - круговая частота - циклическая частота f; - период колабания T; - начальная ( Какова размерность произведения 4. В каких единицах измеряются величины a(t) и Am, если речь идет об электрическом напряжении a(t)=u(t) или токе a(t)=i(t)? 5. Как перейти от гармонического колебания, записанного в синусоидальной форме (3.2) к основной его форме (3.1) так, чтобы при равных t получались одинаковые значения a(t)? Чему при этом следует приравнять величину 6. Vаксимум гармонического колебания u(t) смещен относительно начала развертки осцилографа (рис.3.3) на
Рис. 3.4
8. Два колебания (рис. 3.5) a1(t) и a2(t) выражаются соответственно косинусоидальной и синусоидальной функциями времени
Какое из колебаний отстает от другого по фазе, на какой угол? Изобразите их векторную диаграмму. 9. Чему равна начальная фаза колебания (рис.3.6) и отношение
10. У какого из двух гармонических колебаний разной частоты Рис. 3.6 с другим при одинаковых начальных фазах колебаний
Рис. 3.7
ЗАДАЧИ
3.1. (2 балла). Напряжение и ток в некоторой электрической цепи определяются соответственно двумя гармоническими функциями времени:
Определите значения напряжения и тока в момент времени t=10G мс при следующих параметрах гармонических функций:
Найдите произведение p=p(t)=u(t)·i(t) (мгновенная составляющая тока в цепи в момент времени t) и внесите величину p в милливаттах в АКОС для проверки. 3.2. (2 балла). Приведите к канонической (косинусоидальной) форме три гармонических колебания, заданных функциями
при следующих значениях параметров в градусах:
и найдите их начальные фазы Вычислите сумму 3.3. (2 балла). Найдите параметры гармонического напряжения Um,
Обратите внимание на знак начальной фазы
Рис. 3.8
Напишите выражение для u(t) и вычислите мгновенное значение функции в момент времени t=0. Внесите значение u=u(0) в вольтах для проверки в АКОС. 3.4. (2 балла). Решите поставленную выше задачу 3.3 применительно к другой кривой напряжения (рис. 3.9). По сравнению с рис. 3.8 ось ординат на рис. 3.9 смещена вправо. Найдите в рассматриваемом случае новое значение начальной фазы
Рис. 3.9 3.5. (2 балла). Измеренный на осциллографе (рис. 3.10) интервал времени Определите разность фаз
Рис. 3.10
3.6. (2 балла). Гармоническое колебание задано выражением
где
Изобразите это колебание в виде вектора, подобно изображенному на рис. 3.11. На какой угол q в градусах нужно довернуть против часовой стрелки вектор на рис. 3.11 и во сколько раз (k) увеличить его по длине, чтобы вновь построенный таким путем вектор соответствовал колебанию (3.1)? Внесите величину, равную kq в АКОС для проверки.
ДЛЯ ПЫТЛИВЫХ.
3.1. Составляющие сложного колебания
с частотами w1 и 2w1 испытывают при усилении (рис. 3.12) смещение по фазе
Рис. 3.12
В каком соотношении должны находиться смещения по фазе
ОСНОВНЫЕ ФОРМУЛЫ
ЛИТЕРАТУРА
[1, с. 65 - 71].
ТЕМА 4. ГАРМОНИЧЕСКИЕ ТОК И НАПРЯЖЕНИЕ В ЭЛЕМЕНТАХ ЦЕПИ И ИХ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Гармоническое колебание (напряжение, ток) в общем случае определяется тремя параметрами - амплитудой, частотой и начальной фазой. При известной частоте в расчетах достаточно установить его амплитуду и начальную фазу, что и является обычно
напряжение на нем в соответствии с законом Ома выражается равенством
где
кМежду амплитудами напряжения и тока в сопротивлении R имеет место такое же прямо пропорциональное соответствие (4.3), как между мгновенными значениями в равенстве (4.2). Аналогичная зависимость имеет место по отношению к действующим значениям напряжения UR и тока IR,
Начальная фаза напряжения При токе через L,
напряжение на индуктивности (рис. 4.2) определяется производной от тока
где
- амплитуда напряжения на индуктивности,
- начальная фаза.
Формула (4.7) только по аналогии с (4.3) носит название закона Ома для индуктивности. Начальная фаза напряжения на индуктивности
Формулы (4.7) и (4.10) справедливы только по отношению к амплитудам UmL, ImL или действующим UL, IL значениям напряжения и тока, но ни в коей мере неприменимы к мгновенным значениям uL(t) и iL(t), соотношение между которыми определяется дифференциальным выражением и, кроме того, зависит от времени. При токе через емкость (рис. 4.3)
напряжение на ней, пропорциональное интегралу от тока, равно
Откуда получим закон Ома для емкости:
где xC – модуль реактивного сопротивления емкости, по определению равный:
Реактивное сопротивление емкости (4.14), в отличие от сопротивления индуктивности (4.9), обратно пропорционально частоте w. Начальная фаза напряжения на емкости равна
В емкости ток опережает по фазе напряжение, а напряжение отстает от тока на 900. При последовательном соединении элементов R, L и C (рис. 4.4) мгновенные значения напряжений на элементах складываются алгебраически так, что в любой момент времени результирующее напряжениеu u(t) (рис. 4.4) определяется равенством
u(t)= uR(t)+ uL(t)+ uC(t). (4.16)
Рис. 4.4
Известно, что гармонические колебания одной частоты с разными начальными фазами в сумме образуют гармоническое колебание той же частоты с некоторой результирующей амплитудой Um и начальной фазой
Векторы эти с учетом их угловых положений (начальных фаз) изображены на рис. 4.5а. Здесь же помещен вектор тока Im с начальной фазой
Рис. 4.5
Обозначим через
где
представляет суммарное реактивное сопротивление цепи. Введем, кроме этого, обозначение
где Приняв в качестве опорного вектор тока Из диаграммы и выражений (4.18) и (4.20) следует следует соотношение для амплитуд напряжения и тока:
Введем обозначение
Выражение (4.23) связывает амплитуду Im тока в цепи с амплитудой суммарного напряжения на трех последовательно соединенных элементах в форме закона Ома. Величина Z из (4.22) называется полным сопротивлением цепи с активной (R) и реактивной (X) составляющими. Его величина равна среднеквадратическому значению R и x. Для определения полного сопротивления последовательной RLC цепи ни в коем случае нельзя суммировать R и X по формуле Z=R+X. ЭТО ОШИБКА!!! Реактивное сопротивление X=XL-XC может быть положительно или отрицательно в зависимости от того, какое из сопротивлений XL или XC превалирует. При X> 0 говорят, что сопротивление цепи имеет индуктивный характер, в противном случае (X< 0) - емкостный. Векторная диаграмма на рис.4.5б соответствует индуктивному характеру сопротивления цепи. Возможен случай, когда реактивные сопротивления XL и XC одинаковы по модулю и противоположны по знаку. Тогда они компенсируют друг друга и в соответствии с (4.19) реактивное сопротивление X=0. Такое состояние цепи, зависящее от L, C и частоты сопротивлении Um=UmR. Для описания цепей безотносительно к амплитудам токов и напряжений вводится треугольник сопротивлений, который применительно к цепи с векторной диаграммой рис.4.5б приведен на рис.4.6. Треугольник сопротивлений подобен треугольнику напряжений рис.4.5б и образуется из него путем деления сторон на амплитуду тока Im. Одним катетом треугольника сопротивлений является отрезок, пропорциональный R, другим – X (с учетом знака), а длина гипотенузы равна полному сопротивлению Z цепи. Из рис.4.6 находится сдвиг фаз между напряжением и током
Величина его зависит от параметров цепи и частоты сигнала. Треугольник сопротивлений рис.4.6 соответствует положительным значениям X и
где
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какими выражениями определяются сопротивления элементов цепи R, L и C при гармоническом воздействии?
2. На рис.4.8 приведены три зависимости сопротивлений элементов от частоты. Какие зависимости относятся соответственно к сопротивлениям R, XL и XC? 3. Какая из трех векторных диаграмм тока и напряжения на элементе цепи (рис.4.9) соответствует активному сопротивлению R, индуктивности L, емкости C? Чему равны сдвиги фаз между напряжением и током в этих элементах?
Рис. 4.9
6. Какие из сопротивлений R, XL, XC, X, Z:
|

 в радианах:
в радианах: , (3.5)
, (3.5) , (3.6)
, (3.6)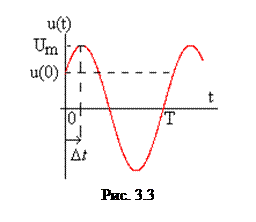 При одном и том же смещении кривых a(t) во времени
При одном и том же смещении кривых a(t) во времени  фазовый сдвиг тем больше, чем меньше период колебаний T и выше частота колебаний
фазовый сдвиг тем больше, чем меньше период колебаний T и выше частота колебаний 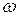 .
.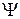 ) фазы?
) фазы? вправо. Чему равна начальная фаза колебания (напишите выражение для нее в общем виде)? Какой знак имеет начальная фаза колебания на рис.3.3?
вправо. Чему равна начальная фаза колебания (напишите выражение для нее в общем виде)? Какой знак имеет начальная фаза колебания на рис.3.3? 7. Чему равен угол сдвига фаз
7. Чему равен угол сдвига фаз 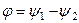 у колебаний, осцилограммы которых приведены на рис. 3.4а? Какая из двух векторных диаграмм (рис. 3.4б или рис. 3.4в) соответствует осцилограммам 1 и 2 на рис. 3.4а?
у колебаний, осцилограммы которых приведены на рис. 3.4а? Какая из двух векторных диаграмм (рис. 3.4б или рис. 3.4в) соответствует осцилограммам 1 и 2 на рис. 3.4а?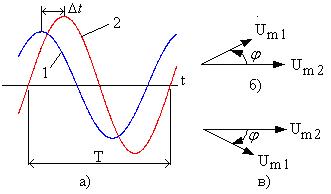


 , если известно, что при t=0 напряжение u(0) отрицательно и равно по абсолютному значению 0, 5 Um?
, если известно, что при t=0 напряжение u(0) отрицательно и равно по абсолютному значению 0, 5 Um?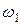 и
и  (T2=T1/2) ближайший максимум напряжения (рис.3.7) дальше отстает от начала координат (интервал
(T2=T1/2) ближайший максимум напряжения (рис.3.7) дальше отстает от начала координат (интервал 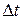 больше) по сравнению
больше) по сравнению
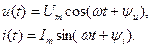
 В,
В,  мА,
мА,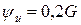 рад,
рад,  рад,
рад,  рад/с.
рад/с.

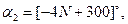

 ,
,  и
и  .
. и внесите ее в АКОС для проверки,
и внесите ее в АКОС для проверки,


 . Сопоставьте с прежним значением
. Сопоставьте с прежним значением  и внесите ее в АКОС для проверки.
и внесите ее в АКОС для проверки.
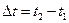 при частоте w=(25+G+N) рад/с равен
при частоте w=(25+G+N) рад/с равен  мс.
мс. двух колебаний в градусах и внесите в АКОС с учетом знака.
двух колебаний в градусах и внесите в АКОС с учетом знака.


 В,
В, град.
град. ,
, 
 ,
,  при соответствующих временных сдвигах
при соответствующих временных сдвигах 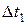 и
и  .
.
 и
и  ;
; 



 При гармоническом токе через сопротивление R (рис. 4.1), описываемом выражением
При гармоническом токе через сопротивление R (рис. 4.1), описываемом выражением , (4.1)
, (4.1) (4.2)
(4.2) (4.3)
(4.3)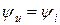 (4.4)
(4.4)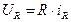 , поскольку
, поскольку 
 (4.4) совпадает с начальной фазой тока через сопротивление R. Это характерно только для сопротивления, называемого активным.
(4.4) совпадает с начальной фазой тока через сопротивление R. Это характерно только для сопротивления, называемого активным. (4.5)
(4.5) и выражается равенством
и выражается равенством (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8) Коэффициент xL, связывающий амплитуды напряжения и тока в формуле (4.7) называется реактивным сопротивлением индуктивности. Величина его зависит от L и w и определяется равенством
Коэффициент xL, связывающий амплитуды напряжения и тока в формуле (4.7) называется реактивным сопротивлением индуктивности. Величина его зависит от L и w и определяется равенством (4.9)
(4.9) .Напряжение опережает по фазе ток, а ток отстает по фазе от напряжения на угол 90°. Аналогичное формуле (4.7) выражение справедливо по отношению к действующим значениям напряжения и тока:
.Напряжение опережает по фазе ток, а ток отстает по фазе от напряжения на угол 90°. Аналогичное формуле (4.7) выражение справедливо по отношению к действующим значениям напряжения и тока: (4.10)
(4.10)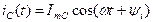 (4.11)
(4.11) . (4.12)
. (4.12)
 (4.13)
(4.13) (4.14)
(4.14)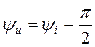 (4.15)
(4.15)
 . (4.17)
. (4.17) совпадают. Векторы
совпадают. Векторы 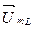 и
и  повернуты относительно тока на угол
повернуты относительно тока на угол  и -
и -  и
и  в последовательной цепи оказываются противоположны по направлению.
в последовательной цепи оказываются противоположны по направлению.
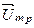 вектор напряжения на реактивных элементах L и C в их последовательном соединении (рис.4.4). Ортогональный (повернутый на
вектор напряжения на реактивных элементах L и C в их последовательном соединении (рис.4.4). Ортогональный (повернутый на  , этот вектор по длине равен
, этот вектор по длине равен (4.18)
(4.18) (4.19)
(4.19) (4.20)
(4.20) - напряжение на активном элементе цепи R.
- напряжение на активном элементе цепи R. , от положения которого зависят другие векторы, можно построить диаграмму в виде (рис. 4.5, б).
, от положения которого зависят другие векторы, можно построить диаграмму в виде (рис. 4.5, б).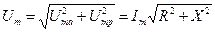 . (4.21)
. (4.21) (4.22)
(4.22) с учетом которого формулу (4.21) можно представить в следующем виде
с учетом которого формулу (4.21) можно представить в следующем виде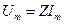 . (4.23)
. (4.23) (4.24)
(4.24)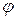 . При отрицательном X соответствующий катет направлен вниз (рис.4.7а) и
. При отрицательном X соответствующий катет направлен вниз (рис.4.7а) и
 Средняя или активная мощность, развиваемая в электрической цепи, зависит от сдвига фаз
Средняя или активная мощность, развиваемая в электрической цепи, зависит от сдвига фаз  , (4.25)
, (4.25) и
и  - действующие значения напряжения и тока. При одинаковых U и I средняя мощность тем выше, чем меньше сдвиг фаз между напряжением и током
- действующие значения напряжения и тока. При одинаковых U и I средняя мощность тем выше, чем меньше сдвиг фаз между напряжением и током  называют коэффициентом мощности. В случае
называют коэффициентом мощности. В случае 
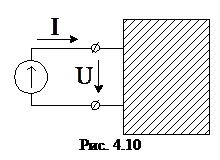 4. При измерениях действующих значений тока I и напряжения U между выводами неизвестного элемента, помещенного в " черный ящик" рис.4.10, выяснилось, что при увеличении частоты источника
4. При измерениях действующих значений тока I и напряжения U между выводами неизвестного элемента, помещенного в " черный ящик" рис.4.10, выяснилось, что при увеличении частоты источника  5. Какой формулой определяется полное сопротивление последовательной RLC цепи Z? Рассмотрите частные случаи, когда цепь состоит из R и L, R и C, L и C. Чему равно полное сопротивление реальной катушки индуктивности, рассматриваемой в виде последовательного соединения R и L (рис.4.11)?
5. Какой формулой определяется полное сопротивление последовательной RLC цепи Z? Рассмотрите частные случаи, когда цепь состоит из R и L, R и C, L и C. Чему равно полное сопротивление реальной катушки индуктивности, рассматриваемой в виде последовательного соединения R и L (рис.4.11)?


