ВВЕДЕНИЕ 1 страница. При изучении учебных курсов по теории электрических цепей необходимо уметь рассчитывать напряжения, токи
При изучении учебных курсов по теории электрических цепей необходимо уметь рассчитывать напряжения, токи, мощности, анализировать характеристики цепей при различных воздействиях. Необходимо освоить различные методы расчета и моделирования цепей с широким применением современной вычислительной техники, приобрести навыки их анализа. Материал пособия разделен на темы, каждая из которых соответствует нескольким лекциям. приведены контрольные вопросы. Первые четыре темы сопровождаются основополагающими теоретическими сведениями для того, чтобы студенты имели возможность выполнять задания даже при отсутствии необходимого лекционного материала. Перед каждым практическим занятием в ходе домашней подготовки студент должен разобраться в теоретическом материале и ответить на контрольные вопросы. В каждой теме содержится по шесть задач. Исходные данные и схемы цепей определяются двумя числами: N - номер студента в списке группы и G - порядковый номер группы по указанию преподавателя. Проверка ответов на задачи производится посредством автоматизированной контролирующей системы АКОС-4, разработанной на кафедре радиотехники.
ТЕМА 1. ИСХОДНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ, ИСТОЧНИКИ НАПРЯЖЕНИЯ И ТОКА
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Во всех радиотехнических устройствах действуют физические процессы, изучаемые в разделе «Электричество» курса физики. Эти знания дают общие представления об электрических устройствах и принципах их действия, однако их недостаточно для специалистов. Так как учебные дисциплины «Основы теории цепей» и «Дополнительные разделы теории цепей» относится к естественным наукам, то для них применим основной метод исследования – метод моделирования. Суть его заключается в том, что для изучения какого-либо физического явления необходимо математическое представление его свойств, которое называется моделью. Модели физических явлений могут обладать различной степенью достоверности описания исследуемых процессов. Так, физические явления в электромагнитном поле могут быть описаны с помощью уравнений теории поля, но такое описание слишком громоздко. Поэтому для инженерных радиотехнических расчетов, там, где это возможно, используется теория электрических цепей, основанная на понятиях тока, напряжения и электродвижущей силы (ЭДС). Электрическим током называется направленное движение заряженных частиц. Так как в металлах носителями заряда являются свободные электроны, то ток в металлах определяется как направленное движение электронов. В полупроводниках имеется два типа зарядов: электроны, имеющие отрицательный заряд, и дырки с положительным зарядом. За положительное направление тока принято направлениедвижения положительных зарядов. В теории цепей часто невозможно определить истинное направление тока
Направление тока характеризуется Рис. 1.1 знаком. Понятие положительный или отри- цательный ток имеет смысл, если только сравнивать направление тока в проводнике с некоторым заранее выбранным ориентиром – положительным направлением тока. Поэтому, если в результате расчета ток будет иметь знак плюс (i> 0), то это означает, что его направление совпадает с выбранным положительным направлением. Если же значение тока i< 0, то его истинное направление противоположно выбранному. Таким образом, выбранное положительное направление тока не означает, что электрические заряды в реальной цепи текут в этом направлении. Оно только придает смысл знаку тока.
прошел заряд q(t), а в момент (t + соответственно q(t+ в момент времени t будет равен
i (t) =
Из выражения (1.1) видно, что ток численно равен скорости изменения заряда, протекающего через заданное сечение проводника S. Никоим образом ток не равен скорости перемещения зарядов.
i(t) =
В этом случае ток называется Рис. 1.3 постоянным. Во всех остальных случаях временных диаграмм q(t) ток будет называться переменным. В Международной системе единиц (СИ) заряд выражается в кулонах (Кл), время в секундах (с), а ток в амперах (А).
Рис. 1.4 ние потенциал Аналогично можно ввести понятие потенциала Напряжением u12 между точками 1 и 2 называется разность потенциалов u12 = представляющая собой работу по переносу единичного положительного заряда из точки 1 в точку 2, которая совершается электрическим полем или внешней силой. Напряжение может быть определено как предел отношения энергии
u12 =
Из определения напряжения следует, что если потенциал точки 1 больше потенциала точки 2, то напряжение u12 будет положительным. Напряжение будет положительным, если оно направлено таким образом, что при переносе положительного заряда
Относительно выбранного положительного направления сравнивают полученный результат. Если полученное напряжение положительно, то истинное направление напряжения совпадает с выбранным. Если же результат будет отрицательным, то истинное направление напряжения будет противоположным. Из сказанного следует, что перед началом расчета обязательно должны быть указаны положительные направления напряжений – только в этом случае возможно их однозначное определение. Положительные направления напряжений выбираются произвольно и независимо от направлений других напряжений и токов в цепи. В Международной системе единиц напряжение имеет размерность вольт (В), а работа (энергия) – джоуль (Дж). Для того чтобы образовать в цепи электрический ток, необходимо какой-либо вид энергии преобразовать в энергию электрического поля от некоторого источника. Например, энергия вращения турбины на электростанции преобразуется в электрическую энергию, подаваемую в розетку потребителя, которая для него выступает источником электроэнергии. Такой источник характеризуется электродвижущей силой (ЭДС), которая может быть определена как работа сторонних сил, затрачиваемая на перемещение единичного положительного заряда внутри источника. Так как ЭДС – это энергия, которую затрачивают сторонние силы на перенос зарядов внутри источника, а напряжение – энергия, расходуемая источником на перенос зарядов в нагрузке, чтобы подчеркнуть их разную сущность, приняли за положительное направление ЭДС направление от точки с меньшим потенциалом к точке с большим потенциалом. Если в цепи положительные направления ЭДС и напряжения на источнике совпадают, то принимают e(t)= - u(t) (рис. 1.6а), а если положительные направления ЭДС и напряжения направлены Рис. 1.5 навстречу друг другу (рис. 1.6б), то e(t) = u(t). Электродвижущая сила (ЭДС) в Международной системе единиц определяется в вольтах. Из выражения (1.2) можно получить
dw = u dq. (1.4)
Учитывая равенство (1.1), имеем
dw = u i dt. (1.5)
Значение энергии dw называется элементарной работой, которую совершает электрическое поле за промежуток времени dt на перенос элементарного заряда dq. Как известно из физики, производная энергии по времени называется мгновенной мощностью
p(t) =
Из (1.6) видно, что мгновенная мощность в электрической цепи может быть как положительной, так и отрицательной. Так, при dw> 0 мощность p(t) положительная, а при dw< 0 мощность p(t) – отрицательная. Из выражения (1.3) имеем, что
p(t) = u i, (1.7)
Чтобы определить энергию, поступившую в цепь к моменту времени t, необходимо выражение (1.6) проинтегрировать по времени
w(t) =
Нижний предел интеграла принят равным (-
всю предысторию поступления электрической энергии в цепь. Если энергия в цепи до момента времени t = t1 была равна нулю, то интеграл (1.8) может быть разбит на два интеграла
w(t) =
так как первый интеграл суммы равен нулю. Необходимо помнить, что значения энергии всегда положительны. Чтобы определить энергию, поступившую в цепь за промежуток времени [t1; ; t2], интегрируется выражение (1.6) в пределах от t1 до t2:
W[t1; t2] =
И, наконец, введем еще одну энергетическую характеристику периодических электрических процессов в цепи – среднюю мощность Р, выделившуюся в цепи за период колебаний
тогда по аналогии получаем
P=
В системе единиц СИ мощность выражают в ваттах (Вт). В технике используются разнообразные источники электрической энергии: химические и солнечные батареи, аккумуляторы, генераторы высокочастотных колебаний и так далее. В теории нет необходимости конкретизировать источники по физическим признакам - вводятся и наделяются определенными свойствами некоторые абстрактные устройства - модели источников, в той или иной мере соответствующие действительно применяемым на практике. Удобно пользоваться двумя типами таких моделей в виде источников напряжения и источников тока. Идеальным источником напряжения называется источник ЭДС e (обозначается кружком с ориентирной стрелкой внутри, рис. 1.6), без внутренних потерь напряжения, независимо от присоединяемой к нему нагрузки и возникающего тока i. Разность потенциалов между точками a, b определяется только ЭДС и остается неизменной при отсоединенной нагрузке (" холостой ход" источника) и при любом ее сопротивлении, теоретически, вплоть до нуля (режим короткого замыкания).
У реального источника напряжения разность потенциалов между выводами в той или иной мере уменьшается с увеличением зависящего от нагрузки тока i. (Вспомните, при включении стартера в автомашине свет меркнет). Для отражения этого факта в модель реального источника напряжения
(рис. 1.6б)) вводят последовательное по отношению к e(t) внутреннее сопротивление источника Re. Теперь напряжение на выходе источника (его нагрузке) оказывается равным
Тогда можно записать выражение для зависимости тока от напряжения
которую принято называть вольтамперной характеристикой реального источника напряжения. Величина Re - фиктивная (расчетная), условно существующая в виде некоторого эквивалентного элемента цепи только в модели реального источника напряжения. Не вздумайте потрошить батарейку или аккумулятор в поисках их внутреннего сопротивления... Выражение (1.12) представляет собой уравнение прямой i=f(u) с отрицательным угловым коэффициентом. Семейство таких прямых при различных внутренних сопротивлениях Re приведено на рис.1.7.
Присмотритесь к прямым (рис. 1.7), сообразуясь с уравнением (1.12). При каком Re вольтамперная характеристика соответствует идеальному источнику напряжения? Какое из неравенств справедливо:
а) Re1< Re2< Re3< Re4, б) Re1> Re2> Re3> Re4?
Максимальное напряжение uxx=e имеет место при холостом ходе источника,
Его можно найти экспериментально посредством двух опытов - холостого хода (измерение напряжения при разомкнутых выводах источника) и короткого замыкания (измерение тока источника при короткозамкнутых выводах), если это физически допустимо. Будьте осторожны при выполнении опыта короткого замыкания источника - его можно производить лишь при уверенности, что внутреннее сопротивление источника достаточно велико и ток не превысит допустимого для источника или амперметра значения. Источником тока называется устройство, модель которого с обозначенным током
Рис. 1.8
У идеального источника тока внутреннее сопротивление Уравнение вольтамперной характеристики источника тока выражается равенством
где Источник тока ведет себя по отношению к выходному току i (через нагрузку) так, как источник напряжения по отношению к выходному напряжению u.
Реальный источник тока тем ближе к идеальному, чем больше его внутреннее сопротивление Ri, в отличие от источника напряжения, у которого для этого требуется, чтобы Re было возможно меньше (в пределе Re=0). Можно подобрать такие значения тока
Рис. 1.9
Таким образом, один и тот же «живой» (физический) источник в зависимости от удобства анализа может быть представлен либо в форме реального источника напряжения, либо источника тока. В качестве источников сигналов часто выступают, кроме генераторов, усилители напряжения и тока. Рассматриваются не абсолютные значения напряжений и токов, а их приращение и соотношения между ними. Электронные усилители могут быть представлены в виде эквивалентных по действию на нагрузку реальных источников тока или напряжения. В силу того, что приращения напряжений и токов в усилителях зависят от управляющих напряжений или токов, такого рода источники называются управляемыми.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.1. ЭДС источника e в цепи на рис.1.10а изменяется по закону e(t)=10cos103t B.
Рис. 1.10
Укажите, потенциал какой точки: 1 или 1', выше в моменты времени t1=1 мс и t2=3 мс. Чему равно напряжение u на элементе цепи z (рис.1.10) при e=e(t1)=5, 4 В: а) при ориентирной стрелке для u (рис. 1.10, а)), проведенной снизу вверх (в том же направлении, что и e); б) при ориентирной стрелке для u (рис. 1.10, б)), проведенной сверху вниз (противоположно e)?
Покажите посредством знаков (+) и (-), потенциал какого конца индуктивности, а или б, выше в этот момент времени. В каком направлении течет ток через индуктивность (рис. 1.11), слева направо или справа налево, если известно, что значение его в момент времени t равно iL=0, 1 А? 1.3. Напишите два выражения для закона Ома (оба справедливые) для двух выбранных направлений ориентирных стрелок u и i на рис. 1.12, а и б соответственно. 1.4. В цепи на рис. 1.13 при положительном напряжении между пластинами конденсатора u, ток i течет в положительном направлении (по стрелке). Какой знак имеет при этом мгновенная мощность P? Происходит ли при этом отбор энергии нагрузкой (конденсатором) от источника, или наоборот?
Рис. 1.12 Рис 1.13
Разберите случай, когда при том же u мгновенная мощность отрицательна (p< 0). Какой знак имеет при этом ток? Какого рода энергетический процесс имеет при этом место – перекачка энергии в нагрузку или возвращение источнику накопленной в нагрузке энергии? 1.5. На рис. 1.14 приведены вольтамперные характеристики двух реальных источников напряжения 1 и 2. У какого из источников - первого или второго - внутреннее сопротивление меньше? Какой из них по своим качествам ближе к идеальному? Напишите, исходя из схемы реального источника, выражения для вольтамперной характеристики. 1.6. На рис. 1.15 приведены две вольтамперные характеристики источников тока. К какому значению внутреннего сопротивления следует стремиться у источника тока с целью его приближения к идеальному? Какая из характеристик, 1 или 2, ближе к характеристике идеального источника? Напишите уравнение вольтамперных характеристик источника тока. Какой вид имеет вольтамперные характеристика идеального источника тока? Почему источники напряжения и тока называются дуальными?
Рис.1.14 Рис. 1.15
1.7. Как изменятся напряжение а) у идеального источника напряжения (рис. 1.16, а)); б) у идеального источника тока (рис. 1.16, б))?
Рис. 1.16
ЗАДАЧИ
1.1 (2 балла). Напряжение между разомкнутыми выводами a и b (рис.1.17а)) при холостом ходе (отсутствии нагрузки) при измерении его посредством вольтметра V оказалось равным uxx=2G·N В.
Рис. 1.17
Ток короткого замыкания Iкз, измеренный (рис. 1.17б)) посредством амперметра с нулевым собственным сопротивлением, оказался равным iкз=(4N+8G)(2+(-1)N+G) А. Постройте по указанным данным характеристику u=f(i) источника. Определите: 1) ЭДС источника E (В); 2) внутреннее сопротивление источника Re (Ом); 3) угол наклона характеристики к оси абсцисс Вычислите величину, равную
и внесите ее для проверки в АКОС (инструкция к вводу данных в АКОС приведена в конце пособия). 1.2 (2 балла). Постройте вольтамперную характеристику и найдите ток короткого замыкания реального источника напряжения (рис. 1.17в)), для которого известно, что при подсоединении к нему нагрузки RH=5G+N(2+(-1)N+G) кОм напряжение на ней стало равным uH=(15GN+8) В. ЭДС источника Е=(20GN+20) В. Значение тока короткого замыкания Iкз (мА) внесите для проверки в АКОС. 1.3 (3 балла). Рассчитайте и постройте вольтамперную характеристику источника тока (рис. 1.18) i=f(uH), для которого известно, что ток его короткого замыкания равен Iкз=(2+0, 1N) ампер, а внутреннее сопротивление Ri=(0, 1N*(4+(-1)N+G)+70) Oм. Определите по характеристике ток через нагрузку i и ее сопротивление RH в Омах, если известно, что напряжение на ней равно uH=(135+G·N/2) B. Внесите найденное сопротивление нагрузки RH в омах в АКОС. 1.4 (3 балла). Постройте вольтамперную характеристику источника (рис. 1.19а) для приращений напряжений и токов Δ u(Δ i) (рис. 1.19б), если известно, что Δ U - линейная функция Δ I. При нулевом значении приращения тока Δ i =0 приращение напряжения равно
Какой вид имеет уравнение вольтамперной характеристики Δ u(Δ i) в данном случае? Напишите его. Определите по характеристике или уравнению приращение тока Δ i, если известно, что напряжение возросло на величину Δ u =(20+G+N) B. Внесите величину Δ i в миллиамперах для проверки в АКОС. 1.5 (1 балл). Укажите, какое значение тока I необходимо установить у источника (рис. 1.20б) для того, чтобы действие источников напряжения (рис. 1.20а)) и тока (рис. 1.20б)) на нагрузку было одинаковым, то есть, чтобы токи и напряжения на одинаковых сопротивлениях нагрузки RH были равны:
|

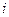 в участке цепи, поэтому ввели условно-положительное направление тока, которое в дальнейшем
в участке цепи, поэтому ввели условно-положительное направление тока, которое в дальнейшем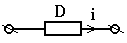 будем называть просто положительным направлением (рис.1.1).
будем называть просто положительным направлением (рис.1.1).
 Количественно ток оценивают по величине заряда q(t), проходящего через какое-либо сечение S проводника (рис. 1.2). Положим, что в момент времени t через поперечное сечение S
Количественно ток оценивают по величине заряда q(t), проходящего через какое-либо сечение S проводника (рис. 1.2). Положим, что в момент времени t через поперечное сечение S t) Рис. 1.2
t) Рис. 1.2
 =
=  . (1.1)
. (1.1) В общем случае ток является функцией времени. Временная зависимость тока может подчиняться различным законам. В частном случае, когда зависимость заряда от времени представляет собой линейную функцию
В общем случае ток является функцией времени. Временная зависимость тока может подчиняться различным законам. В частном случае, когда зависимость заряда от времени представляет собой линейную функцию  (временная диаграмма приведена на рис. 1.3) скорость изменения заряда во времени представляет собой постоянную величину I. Из (1.1) видно, что в таком случае
(временная диаграмма приведена на рис. 1.3) скорость изменения заряда во времени представляет собой постоянную величину I. Из (1.1) видно, что в таком случае =
=  = I = const.
= I = const.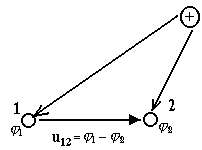 Из физики известно, что на всякий заряд, помещенный в электрическом поле, действует сила, которая зависит от напряженности электрического поля, величины заряда и его знака. При движении единичного положительного заряда из бесконечности в точку 1 (рис. 1.4) будет затрачена (источником электри-ческого поля) или выделена энергия, которая носит назва-
Из физики известно, что на всякий заряд, помещенный в электрическом поле, действует сила, которая зависит от напряженности электрического поля, величины заряда и его знака. При движении единичного положительного заряда из бесконечности в точку 1 (рис. 1.4) будет затрачена (источником электри-ческого поля) или выделена энергия, которая носит назва-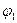 точки 1.
точки 1. для точки 2.
для точки 2. из точки 1 в точку 2,
из точки 1 в точку 2,
 =
=  . (1.3)
. (1.3)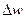 на его перенос от точки с большим потенциалом к точке с меньшим потенциалом.
на его перенос от точки с большим потенциалом к точке с меньшим потенциалом. За положительное направление напряжения принимается направление от точки с большим потенциалом к точке с меньшим потенциалом. При расчете электрических цепей чаще всего не удается заранее определить направление напряжения, поэтому до начала расчета вводят условно-положительное направление напряжения.
За положительное направление напряжения принимается направление от точки с большим потенциалом к точке с меньшим потенциалом. При расчете электрических цепей чаще всего не удается заранее определить направление напряжения, поэтому до начала расчета вводят условно-положительное направление напряжения. . (1.6)
. (1.6) . (1.8)
. (1.8) ), чтобы учесть
), чтобы учесть =
= 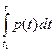 , (1.9)
, (1.9) . (1.10)
. (1.10) . В математике вводится понятие среднего значения периодической функции
. В математике вводится понятие среднего значения периодической функции =
= 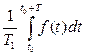 .
.
 . (1.11)
. (1.11)
 .
. . (1.12)
. (1.12)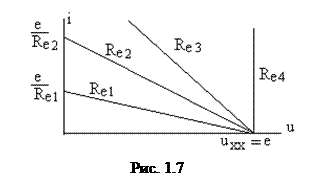
 , максимальный ток
, максимальный ток  - при коротком замыкании его выводов. Внутреннее сопротивление может быть определено из очевидного равенства
- при коротком замыкании его выводов. Внутреннее сопротивление может быть определено из очевидного равенства (1.13)
(1.13) приведена на рис. 1.8а, вольтамперная характеристика - на рис. 1.8б, Rj – внутреннее сопротивление источника тока.
приведена на рис. 1.8а, вольтамперная характеристика - на рис. 1.8б, Rj – внутреннее сопротивление источника тока.
 - из схемы его следует убрать. Идеальный источник тока отличается тем, что генерируемый им ток не зависит от сопротивления нагрузки RH, а следовательно, и от напряжения на нагрузке u, о чем говорит горизонтальная прямая при
- из схемы его следует убрать. Идеальный источник тока отличается тем, что генерируемый им ток не зависит от сопротивления нагрузки RH, а следовательно, и от напряжения на нагрузке u, о чем говорит горизонтальная прямая при  на рис.1.8б. У реального источника происходит перераспределение токов через Ri и Rн в пользу нагрузки с уменьшением ее сопротивления.
на рис.1.8б. У реального источника происходит перераспределение токов через Ri и Rн в пользу нагрузки с уменьшением ее сопротивления. , (1.14)
, (1.14) - внутренняя проводимость источника тока. Уравнения (1.14) и (1.12) дуальны в том смысле, что одно из них может быть получено из другого путем замены e на i и Re на G i. Соответственно этому, источники напряжения и тока называются дуальными.
- внутренняя проводимость источника тока. Уравнения (1.14) и (1.12) дуальны в том смысле, что одно из них может быть получено из другого путем замены e на i и Re на G i. Соответственно этому, источники напряжения и тока называются дуальными. у реальных источников, чтобы при одинаковых Ri=Re=Rист их действие на нагрузку (напряжение на нагрузке и протекающий через нее ток) было одинаковым, как показано на рис. 1.9. Условия эквивалентности таковы:
у реальных источников, чтобы при одинаковых Ri=Re=Rист их действие на нагрузку (напряжение на нагрузке и протекающий через нее ток) было одинаковым, как показано на рис. 1.9. Условия эквивалентности таковы: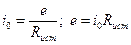 (1.15)
(1.15)

 1.2. Вычисленное значение напряжения на индуктивности L (рис. 1.11) в некоторый момент времени t равно uL=10 В.
1.2. Вычисленное значение напряжения на индуктивности L (рис. 1.11) в некоторый момент времени t равно uL=10 В.

 на нагрузке u и ток
на нагрузке u и ток 



 (рад).
(рад). ,
, B. При нулевом приращении напряжения (Δ u =0) приращение тока равно
B. При нулевом приращении напряжения (Δ u =0) приращение тока равно 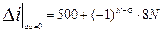 мА.
мА.
 ,
,  .
.


