ВВЕДЕНИЕ 6 страница. Внесите в АКОС для проверки значения:
Внесите в АКОС для проверки значения: LЭ, миллигенри - для студентов с четными номерами N при N≤ 13; CЭ, нанофарад - для студентов с нечетными номерами N при N≤ 13; RЭ, ом - для студентов с четными и нечетными N при N> 13. 8.3. (2 балла). Найдите эквивалентное сопротивление цепи (рис.8.15) ZЭ = RЭ + jXЭ = Z при следующих данных: XL = (150 + (-1)N 2 (N - G)) Ом, XC = (100 + 2 N + 2 G) Ом, R = (400 + (-1)N+G 4 (N + G)) Ом.
Рис. 8.15 Внесите в АКОС для проверки величину XЭ в омах со знаком минус, если она имеет емкостный характер, или со знаком плюс в противном случае. 8.4. (1 балл). Преобразуйте источник Э.Д.С. (рис.8.16, а) в эквивалентный источник тока (рис.8.16, б) так, чтобы напряжения на нагрузке
Ze = (200 + 50 G - 4 N) exp(j N G0) Ом.
Амплитуду тока эквивалентного источника ImЭ в милли-амперах внесите для проверки в АКОС.
Рис.8.16
8.5. (2 балла). В схеме (рис.8.17) методом преобразования источника тока Рис. 8.17 Дано:
Амплитуду тока через емкость 8.6. (3 балла). Используя теорему Тевенена, преобразуйте цепь (рис.8.18, а) относительно ветви R (выходные узлы
Рис. 8.18
Вычислите по эквивалентной схеме (рис.8.18, б) напряжение на R при следующих данных:
R = R1 = R2 = R3 = (100 + (-1)N 2 N) Ом,
Внесите величину UR, в вольтах в АКОС для проверки.
ДЛЯ ПЫТЛИВЫХ
8.1. При каком соотношении сопротивлений Z1, Z2, Z3 и Z4
Рис. 8.19
Рис. 8.20
8.3. Решите задачу 8.2 " для пытливых", заменив в схеме на рис. 8.20 активные сопротивления R1, R2, R3, R4 и R5 комплексными сопротивлениями Z1, Z2, Z3, Z4 и Z5. Изменятся ли и каким образом возможные решения задачи?
ТЕМА 9. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какими величинами характеризуется индуктивная связь между катушками? Их обозначения, размерности, в каких пределах заключены возможные значения? 2. Какие меры конструктивного характера принимаются для: - уменьшения рассеяния и увеличение коэффициента связи между катушками; - уменьшения энергетических потерь в сердечнике и проводах катушек? 3. Какими выражениями определяются в общем случае вносимая ЭДС и напряжение между разомкнутыми выводами второй катушки при протекании произвольного по форме тока в первой катушке? От чего зависят их величина и направление?
5. Какая из осциллограмм напряжения
Рис. 9.2
6. В каких амплитудных и фазовых соотношениях находятся напряжение на выходе второй катушки с гармоническиv током в первой? Какая величина называется сопротивлением связи? Чему равны: - амплитуда выходного напряжения при заданной амплитуде тока в первой катушке; - начальная фаза выходного напряжения при заданной фазе первичного тока? В каком соотношении находятся комплексные амплитуды выходного напряжения и тока в первой катушке?
8. Какое соединение двух последовательно включенных катушек называется согласным, встречным? Чему равны эквивалентные индуктивности двух согласно и встречно включенных катушек с взаимной индуктивностью?
Рис. 9.3
9. Объясните принцип действия вариометра. Для каких целей он используется. В каком диапазоне можно изменять эквивалентную индуктивность вариометра при вращении второй катушки относительно первой? 10. Какой трансформатор называется идеальным? Каким требованиям должен удовлетворять идеальный трансформатор?
тельно к схеме (рис.9.4). 12. В каком соотношении находятся входные и выходные напряжения у идеального трансформатора? Входной и выходной токи? 13. С какой целью в линиях электропередачи (ЛЭП) повышается напряжение? 14. Какое сопротивление у трансформатора называется входным? Как зависит входное сопротивление трансформатора от его нагрузки? Чем определяется его выходное сопротивление? Напишите формулы для входного и выходного сопротивлений трансформатора. 15. О чем говорит название " согласующий трансформатор"? Для чего он применяется? Из каких соображений выбирается соотношение витков первичной и вторичной обмоток у согласующего трансформатора? 16. В чем состоит свойство обратимости (взаимности) в линейных цепях? Как оно проявляет себя в электрическом трансформаторе? 17. Каким простейшим способом можно изменить фазу выходного напряжения на 180 по сравнению с входным посредством трансформатора? 18. Объясните устройство и принцип действия автотрансформатора. Сравните его по эксплуатационным и конструктивным показателям с трансформатором.
ЗАДАЧИ
9.1. (1 балл). Вычислите коэффициент связи
L1 = (600 + (-1)N+G N G)) мГн, L2 = (200 + N G) мГн, M = (90 + (-1)N (N + G)) мГн,
Рис. 9.5 Определите сопротивление связи ме- жду катушками проверочной целью контрольную величину
e(t)=Em cos(ω t +ψ e), Em = (2 N + 5 G)/2 В, Рис. 9.6 ψ e = -[(N + G)/2]0. Найдите значение 9.3. (3 балла). Определите комплексную амплитуду тока во второй катушке
L2 = (200 - (-1)(N+G) N) мГн,
Z2 = (2000 + 2 N + 5 G) Ом,
Рис.9.7 9.4. (2 балла). Определите комплексную амплитуду тока во второй катушке
L1 = (500 + (-1)N N G) мГн, L2 = (200 + N G) мГн, M = (150 + (-1)N+G 2 N) мГн, R1 = (200 + 2 G2) Ом, R2 = (600 – 2 N G) Ом, Em0= (250 + 50 G - N) В,
Рис. 9.8 Амплитуду тока 9.5. (2 балла). Определите соотношение чисел витков
обмоток идеального трансформатора, необходимое для того, чтобы при токе I2 через нагрузку R2 входной ток трансформатора I1 (рис.9.9) не превосходил 0, 5 А,
I2= (600 + (-1)N N G) мА, R2 = (500 + 5 N G) Ом.
Определите входное сопротивление трансформатора при указанном R и внесите его в омах в АКОС для проверки. Рис. 9.9
9.6. (2 балла). Найдите коэффициент трансформации согласующего трансформатора (рис.9.10)
Re = (500 + N (13 - G)) Ом, Рис.9.10
R2 = (40 + (-1)N 0, 5 (N + G)) кОм.
Значение 103
ДЛЯ ПЫТЛИВЫХ
9.1. Определите ток в нагрузке
Рис.9.11
ОСНОВНЫЕ ФОРМУЛЫ
ЦЕПЕЙ
КОНТРОЛЬНЫЕ ВОПРОСЫ
10.1. Какие методы определения напряжений и токов в ветвях цепи Вам известны? Назовите их. В чем заключается метод токов ветвей? Какое необходимое и достаточное количество линейно независимых уравнений электрического равновесия необходимо для решения задачи о токах в а) при условии, что ветви не содержат идеальных источников тока; б) в 10.2. Образуйте систему линейно независимых уравнений для определения токов в ветвях цепи, схема которой приведена на рис.10.1, а, а топологический граф - на рис.10.1, б. Какое количество уравнений необходимо составить для этой цели? Сколько уравнений достаточно для решения задачи о неизвестных токах в цепи (рис.10.1, в) с идеальным источником тока в правой ветви?
Рис.10.1
10.3. Какое число независимых уравнений необходимо ввести в систему для решения задачи о токах в ветвях цепи, топологический граф которой приведен на рис. 10.2? Какое число их Рис.10.2 состоит?
10.4. В чем заключается метод контурных токов, применяемый для определения напряжений и токов в цепях? Какие токи называются контурными? Обозначьте их на чертеже (рис.10.3) и образуйте систему независимых уравнений по методу контурных токов применительно к этой цепи. Какое количество уравнений у Вас получилось? Сравните с методом токов ветвей в вопросе 10.2? 10.5. Составьте уравнение электрического равновесия в соответствии с вторым законом Кирхгофа для цепи на рис. 10.4, не прибегая к преобразованию источника тока в эквивалентный источник напряжения.
Рис.10.3 Рис.10.4
10.6. Объясните на примере цепи рис.10.5, в чем состоит метод узловых потенциалов? Относительно каких искомых величин формируется система независимых уравнений при этом методе?
Рис. 10.5
ного и смежных узлов Рис. 10.6
10.7. Составьте уравнение равновесия для токов в узле 2 цепи рис.10.5. Выразите токи ветвей через искомые узловые потенциалы данного и смежных узлов. 10.8. Составьте выражение для баланса токов в узле 3 цепи рис.10.5, выразите токи ветвей через узловые потенциалы. 10.9. По результатам работы над вопросами 10.6 - 10.8 запишите систему уравнений по методу узловых потенциалов для всей цепи рис.10.5. 10.10. Образуйте два уравнения по методу контурных токов для цепи рис.10.7, а. Убедитесь в том, что уравнения имеют такой вид, как если бы они были составлены из двух индуктивно связанных контуров (рис. 10.7, б), и схема рис.10.7, а может служить схемой замещения цепи с взаимной индуктивностью.
Рис. 10.7
ЗАДАЧИ
10.1. (1 балл). Определите комплексные амплитуды контурных токов R1 = (2 G + N/2) Ом, R2 = (90 + (-1)N 2 N) Ом, R12 = (50 + (-1)N+G N+G) Ом, Рис.10.8 Значение амплитуды тока 10.2. (1 балл). Составьте систему уравнений по методу узловых потенциалов, найдите потенциалы узлов рис. 10.9: G10= 1/(2 G + N/2) Сим, G20= 1/(90 + (-1)N 2 N) Сим, G12= 1/(50 + G + (-1)N+G N) Сим,
Рис.10.9
Амплитуду разности потенциалов 10.3. (3 балла). Для цепи рис.10.10 составьте систему независимых уравнений по методу контурных токов. Решите систему уравнений относительно контурных токов
Группы 1, 3, 5, 7
Группы 2, 4, 6, 8
R1 = (0, 5 N + G) Ом, R2 = (0, 4 N + 2 G) Ом, R3 = (4 G + N)Ом, R12 = (0, 5 N + 20) Ом, R13 = (10 + (-1)N 0, 2 N) Ом, R23=(30 + (-1)N+G 0, 5N) Ом, Полученные значения амплитуды тока Рис. 10.10 проверки в АКОС.
10.4. (3 балла). Для цепи рис.10.1 составьте систему 1уравнений по методу узловых потенциалов и найдите амплитуду разности потенциалов
Группы 1, 3, 5, 7
Группы 2, 4, 6, 8
G2 = 1/(2 N + 5 G) Сим, G3 = G/(60 + (-1)N N) Сим, G12 = 4/(150 + N G) Сим, G13 = 1/(60 + (-1)N N) Сим, G23 =(N +G)/(20 + N2) Сим,
Найденное значение амплитуды
10.5. (2 балла). Для цепи рис.10.12 составьте систему уравнений для определения контурных токов указаны ниже. Рис. 10.12
Группы 1, 3, 5, 7
|



 и токи через нее при равных
и токи через нее при равных 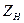 были одинаковыми, при следующих данных:
были одинаковыми, при следующих данных: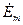 = 1000 |sin(N G рад)| В,
= 1000 |sin(N G рад)| В,
 в эквивалентный источник ЭДС
в эквивалентный источник ЭДС  найдите ток через емкость
найдите ток через емкость  для четных N или ток через индуктивность
для четных N или ток через индуктивность  для нечетных N.
для нечетных N. = (100 + 2 N + 4 G) Ом, ZL= (300 – 2 N – G2) Ом,
= (100 + 2 N + 4 G) Ом, ZL= (300 – 2 N – G2) Ом, = (200 +2 N + G2) Ом.
= (200 +2 N + G2) Ом. для четных N или индуктивность
для четных N или индуктивность 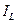 для нечетных N в миллиамперах внесите в АКОС для проверки.
для нечетных N в миллиамперах внесите в АКОС для проверки. ) в эквивалентный источник ЭДС
) в эквивалентный источник ЭДС  так, чтобы напряжение на сопротивлении R в исходной (рис.8.18, а) и эквивалентной (рис.8.18, б) схемах было одинаковым.
так, чтобы напряжение на сопротивлении R в исходной (рис.8.18, а) и эквивалентной (рис.8.18, б) схемах было одинаковым.
 = (0, 2 + 0, 02 G) А,
= (0, 2 + 0, 02 G) А,  = (800 + (-1)N+G 8 (N + G)) В.
= (800 + (-1)N+G 8 (N + G)) В. замыкание или размыкание ключа не приведет к изменению токов ни в одной из ветвей цепи на рис.8.19? Чему при этом равны напряжения на разомкнутом ключе и ток через замкнутый ключ?
замыкание или размыкание ключа не приведет к изменению токов ни в одной из ветвей цепи на рис.8.19? Чему при этом равны напряжения на разомкнутом ключе и ток через замкнутый ключ? 8.2. В схеме цепи рис.8.20 через сопротивление R5 протекает ток
8.2. В схеме цепи рис.8.20 через сопротивление R5 протекает ток  4. Какие концы двух катушек называются одноименными? Определите, какой из концов катушки (а или б) является одноименным помеченному на чертеже (рис.9.1) звездочкой концом первой катушки, если известно, что при замыкании ключа K стрелка гальванометра отклонилась вправо? В какую сторону сдвинется стрелка при размыкании ключа K? Рис. 9.1
4. Какие концы двух катушек называются одноименными? Определите, какой из концов катушки (а или б) является одноименным помеченному на чертеже (рис.9.1) звездочкой концом первой катушки, если известно, что при замыкании ключа K стрелка гальванометра отклонилась вправо? В какую сторону сдвинется стрелка при размыкании ключа K? Рис. 9.1 (1-4) на рис.9.2, б соответствует току
(1-4) на рис.9.2, б соответствует току  на рис.9.2, а?
на рис.9.2, а?
 7. На рис.9.3 изображен вектор тока в первой катушке
7. На рис.9.3 изображен вектор тока в первой катушке  . Какой из восьми других векторов соответствует напряжению на выходе второй катушки? Назовите его номер.
. Какой из восьми других векторов соответствует напряжению на выходе второй катушки? Назовите его номер. 11. Посредством каких двух уравнений можно решить задачу определения первичного и вторичного токов в трансформаторе при включенной нагрузке? Напишите их примени- Рис. 9.4
11. Посредством каких двух уравнений можно решить задачу определения первичного и вторичного токов в трансформаторе при включенной нагрузке? Напишите их примени- Рис. 9.4 между катушками L1 и L2 (рис.9.5) при следующих данных:
между катушками L1 и L2 (рис.9.5) при следующих данных:
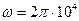 рад/с.
рад/с. . Вычислите с
. Вычислите с в омах и внесите ее в АКОС для проверки.
в омах и внесите ее в АКОС для проверки. 9.2. (2 балла). Определите при указанных в задаче 9.1.
9.2. (2 балла). Определите при указанных в задаче 9.1. данных ток
данных ток  в цепи рис. 9.7 при значениях:
в цепи рис. 9.7 при значениях: = (1, 5 + (-1)N 0, 01 (N + G)) А,
= (1, 5 + (-1)N 0, 01 (N + G)) А, ZСВ = ω M = (5 G + N + 200) Ом,
ZСВ = ω M = (5 G + N + 200) Ом,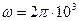 рад/с.
рад/с. Внесите для проверки в АКОС величину, равную
Внесите для проверки в АКОС величину, равную  , где
, где  - начальная фаза тока (радиан).
- начальная фаза тока (радиан). цепи (рис.9.8) при следующих данных:
цепи (рис.9.8) при следующих данных: рад/с.
рад/с.
 необходимый для того, чтобы входное сопротивление трансформатора (между точками а, б) было равно сопротивлению источника Re,
необходимый для того, чтобы входное сопротивление трансформатора (между точками а, б) было равно сопротивлению источника Re, внесите в АКОС для проверки.
внесите в АКОС для проверки.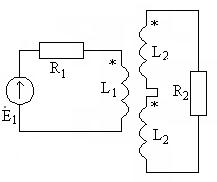





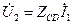





 ТЕМА 10. РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ
ТЕМА 10. РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ветвях:
ветвях: из
из 
 может быть получено, исходя из первого закона Кирхгофа? Из второго закона Кирхгофа? В цепи рис.10.2 выделите 11 контуров (1-2; 2-3-4; 2-3-6-5; 1-3-7-5 и др.). Каким правилом можно воспользоваться при выборе необходимого числа контуров для системы линейно независимых уравнений? В чем оно
может быть получено, исходя из первого закона Кирхгофа? Из второго закона Кирхгофа? В цепи рис.10.2 выделите 11 контуров (1-2; 2-3-4; 2-3-6-5; 1-3-7-5 и др.). Каким правилом можно воспользоваться при выборе необходимого числа контуров для системы линейно независимых уравнений? В чем оно


 Как связано необходимое для системы число уравнений с топологией цепи (количеством узлов)? Образуйте уравнение электрического равновесия (баланса токов) в узле 1 цепи (рис.10.5), представленном отдельно на рис.10.6. Выразите токи через искомые узловые потенциалы дан-
Как связано необходимое для системы число уравнений с топологией цепи (количеством узлов)? Образуйте уравнение электрического равновесия (баланса токов) в узле 1 цепи (рис.10.5), представленном отдельно на рис.10.6. Выразите токи через искомые узловые потенциалы дан-
 и
и 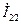 в цепи на рис. 10.8 и найдите ток
в цепи на рис. 10.8 и найдите ток  через сопротивление
через сопротивление  . Значения сопротивлений и комплексной амплитуды ЭДС источника примите равными:
. Значения сопротивлений и комплексной амплитуды ЭДС источника примите равными: в миллиамперах занесите для проверки в АКОС.
в миллиамперах занесите для проверки в АКОС. ,
,  и их разность
и их разность  при следующих данных для цепи на
при следующих данных для цепи на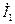 = (0, 01 G) А,
= (0, 01 G) А,  = (0, 01 N / G) А.
= (0, 01 N / G) А.
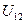 в милливольтах занесите для проверки в АКОС.
в милливольтах занесите для проверки в АКОС. и определите токи в ветвях
и определите токи в ветвях  . Индексы
. Индексы  и
и  в зависимости от номера группы G и Вашего номера N в системе группы примите равными:
в зависимости от номера группы G и Вашего номера N в системе группы примите равными: Значения сопротивлений в цепи и ЭДС источника равны:
Значения сопротивлений в цепи и ЭДС источника равны: в миллиамперах внесите для
в миллиамперах внесите для между узлами
между узлами  Все проводимости в цепи активные. При вычислениях воспользуйтесь следующими данными:
Все проводимости в цепи активные. При вычислениях воспользуйтесь следующими данными: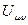 (в милливольтах) внесите для Рис.10.11
(в милливольтах) внесите для Рис.10.11 проверки в АКОС.
проверки в АКОС. в ветви номер
в ветви номер 


