ВВЕДЕНИЕ 7 страница. Значения сопротивлений ветвей, ЭДС и тока источников примите равными:
Группы 2, 4, 6, 8
Значения сопротивлений ветвей, ЭДС и тока источников примите равными:
R1 = (N + G) Ом, R2= (0, 5 N + 2 G) Ом, R12 = (50 + (-1)N N) Ом, R13 = (G + 0, 5 N) Ом, R23 = (50 - N) Ом,
Найденное значение амплитуды тока
Рис. 10 13
G10 = 1/(30 + (-1)N 0, 5 N) Сим, G12 = 1/(G + 0, 3 N) Сим, G13 = 1/(12 + (-1)N 0, 2 N) Сим, G20 = 1/(0, 5 N + G) Сим, G23 = 1/(12 + 0, 2 N) Сим,
Найденное значение амплитуды тока
ТЕМА 11. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ЦЕПИ ПЕРВОГО ПОРЯДКА
КОНТРОЛЬНЫЕ ВОПРОСЫ
11.1. Дайте определение комплексного коэффициента передачи четырехполюсника, его амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик. 11.2. К какому типу фильтров относятся показанные на рис. 11.1 четырехполюсники? Получите выражения для их АЧХ и ФЧХ, постройте графики.
Рис. 11.1
11.3. Дайте определение полосы пропускания частотного фильтра. Что представляет собой полоса удержания? К каким частотным фильтрам они относятся? 11.4. Рассчитайте полосу пропускания (удержания) для показанных на рис. 11.1 фильтров. Как влияют на них параметры цепей. 11.5. Как определяется коэффициент прямоугольности частотного фильтра? Проведите необходимые расчеты для по- казанных на рис. 1 цепей. 11.6. Исследуйте влияние нагрузки
Рис. 11.2
11.7. Постройте качественно (не проводя расчетов) АЧХ фильтров, схемы которых показаны на рис. 11.3, используя свойства реактивных элементов на очень низких и высоких частотах.
Рис. 11.3
ЗАДАЧИ
11.1 (2 балла). В схеме рис. 11.4 установите ключи К1 - К4 в положения, соответствующие двоичному коду Вашего номера N в списке группы (таблица приведена в конце руко-водства). Оставьте в схеме только те элементы, на которые указывают стрелки после установки ключей, а остальные удалите, замкнув образовавшиеся разрывы. Полученную схему занесите в свою рабочую тетрадь. Параметры цепи примите равными: R = 0, 5(N +2 G) кОм, L = 0, 5 N мГн, C = N пФ.
Рис. 11.4
Присмотритесь к построенной Вами характеристике - соответствует ли она Вашим физическим представлениям о частотно-избирательных свойствах рассматриваемой цепи. Определите величину H=1000 H(ω) при частоте источника ω =(1/G)· 107 рад/с и введите ее в АКОС для проверки. Задача 11.2 (2 балла). Получите применительно к Вашей схеме и указанным выше данным формулу для определения фазо-частотной характеристики (ФЧХ) - зависимости от частоты сдвига фаз φ (ω) между выходным и входным напряжениями. Рассчитайте и постройте график ФЧХ в том же масштабе частот, что и АЧХ в предыдущей задаче. Определите значение φ =10 φ (ω) в градусах на частоте ω =(1/G)· 107 рад/с и внесите его в АКОС. Задача 11.3 (1 балл). Представьте выражение для напряжения на выходе Вашей цепи в тригонометрической форме
u2 (t) = Umcos(ω t+ψ 2)
при напряжении на входе, равном
u(t)=1cos(2π · 106t - π /6) В.
Вычислите величины Um2 и ψ 2 и подставьте их в выражение для u2(t). Найдите значение u2(t) (милливольт) при t=0 и внесите ответ для проверки в АКОС. Задача 11.4 (2 балла). Обратитесь к схеме цепи рис.11.5. Положим, что на ее вход поступает смесь двух напряжений - постоянного и переменного, сумму которых запишем в виде
uвх(t)=U0+Umcos(ω t+ψ).
Примем, что уровни постоянного и переменного напряжений на входе цепи одинаковы, то есть U0=Um Определите отношение амплитуды переменной составляющей выходного напряжения к величине его постоянной составляющей,
при условии, что частота входного переменного напряжения равна f=50 Гц и R=(N+5G) кОм, C=(3N+5)/G мкФ. Вычислите значение Задача 11.5 (2 балла). Найдите, какое минимальное значение емкости конденсатора C=C1 необходимо использовать в цепи рис. 11.5 при R=(N+5G) кОм и частоте f=50 Гц для того, чтобы величина Kвых из задачи 11.4 не превосходила 0, 05 (пяти процентов). Найденное значение C 1 в нанофарадах внесите в АКОС.
и его модуль на частоте источника ω =106 рад/с при R2=0, 1G кОм, L=(N + 2 G) мГн.
Величину модуля проходного сопротивления в Омах внесите в АКОС для проверки.
ТЕМА 12. ПОСЛЕДОВАТЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР
КОНТРОЛЬНЫЕ ВОПРОСЫ
12.1. Опишите явление резонанса напряжений в последовательном колебательном контуре. Каковы условия его возникновения? Чему равны в этом случае реактивное и полное комплексное сопротивления контура, как они меняются в окрестности резонансной частоты? 12.2. Каким выражением определяется комплексный коэффициент передачи последовательного колебательного контура при снятии выходного напряжения с емкости и индуктивности? Чему равны его АЧХ и ФЧХ? 12.3. Запишите формулы для резонансной частоты, резонансного и характеристического сопротивления, добротности и полосы пропускания контура. Каков физический смысл этих величин? 12.4. Как выглядят графики АЧХ и ФЧХ последовательного колебательного контура? Как влияют его параметры на форму частотных характеристик? 12.5. Дайте определение обобщенной расстройки контура, каким приближенным выражением она определяется, каков ее физический смысл? 12.6. Запишите в координатах обобщенной расстройки выражения для входного сопротивления, комплексного коэффициента передачи, АЧХ и ФЧХ последовательного колебательного контура. 12.7. Как отображаются графически в координатах обобщенной расстройки АЧХ и ФЧХ последовательного колебательного контура? Как влияют на форму кривых параметры цепи? 12.8. Как влияет нагрузка на частотные характеристики контура? Каковы требования к величине сопротивления нагрузки? ЗАДАЧИ
Задача 12.1 (2 балла). Определите резонансную частоту ω 0, характеристическое сопротивление ρ и добротность Q последовательного колебательного контура, при следующих исходных данных: R = (G + 0, 2N) Ом, L = (50 + NG) мкГн, C=(1500 – (-1)N 3 N G) пФ. Вычислите значения ω 0 (радиан делить на секунду), ρ (Ом) и Q. Введите для проверки в АКОС контрольную величину
Задача 12.3 (2 балла). Допустим, что на вход последовательного колебательного контура поступает одновременно два напряжения - от полезной (Uпол) и мешающей (Uмеш) радиостанций. Определите коэффициент ослабления
представляющий собой частное отношений уровней мешающего сигнала к полезному на входе и выходе контура. Он показывает, во сколько раз относительный уровень мешающего сигнала (по сравнению с полезным) на выходе контура меньше, чем на входе. Примите, что: а) контур с параметрами из задачи 12.1 настроен в резонанс с сигналом полезной станции, работающей на частоте ω пол=ω 0; б) частота сигнала мешающей станции равна ω меш=ω 0+kП, где к=0, 3G+0, 05N; в) на входе контура напряжения от обеих станций имеют одинаковые амплитуды Uполвх=Uмешвх. Величину 1000· η введите в АКОС для проверки. Задача 12.4 (2 балла). Известно, что амплитудно-модулированное одним тоном колебание может быть представлено в виде суммы трех гармонических составляющих с амплитудами U0, U1Б, U2Б, где U0 - амплитуда колебания несущей частоты f0, U1Б и U2Б - равные по величине амплитуды так называемых боковых составляющих модулированного сигнала с частотами f0-fM и f0+fM соответственно, fM - частота модулирующего гармонического напряжения. Спектр тонально-модулированного колебания в виде трех вертикальных линий, высота которых пропорциональна амплитудам составляющих, исходящих из соответствующих точек на оси частот, показан на рис.12.1. Определите, какую добротность Q должен иметь колебательный контур, настроенный на частоту f0, для того, чтобы все три составляющих модулированного сигнала точно «вписались» в полосу пропускания контура при следующих исходных данных:
f0=(1000 +(-1)N 2GN)· 104 Гц, fM=(500 - (-1)N GN) · 102 Гц.
Полученное значение Q введите в АКОС.
амплитудно-модулированные сигналы (описанные в предыдущей задаче) от двух радиостанций с несущими частотами f0 и f0+F соответственно, где величину F называют разносом частот. Спектр сигналов (по аналогии с задачей 12.4) показан на рис. 12.2. Контур настроен на частоту f0 и имеет добротность Q=100. При данных задачи 12.4 определите, какой разнос частот F необходимо установить для того, чтобы составляющие сигнала от соседней станции ослаблялись контуром не менее, чем в 100 раз по сравнению с колебанием на частоте настройки контура f0. Значение F в килогерцах введите в АКОС. Задача 12.6 (2 балла). Какими максимальным (Cmax) и минимальным (Cmin) значениями емкости должен обладать конденсатор переменной емкости контура для перекрытия диапазона частот настройки от fmin до fmax при следующих данных: L=(10 + 0, 1N) Г, fmin=(2+ N· G/50)· 106 Гц, fmax=(5 + N· G/30)· 106 Гц. Величину α =1000(Cmax / Cmin) внесите в АКОС для проверки.
ТЕМА 13. ПАРАЛЛЕЛЬНЫЙ И СВЯЗАННЫЕ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ
КОНТРОЛЬНЫЕ ВОПРОСЫ
13.1. В чем заключается явление резонанса токов в параллельном колебательном контуре? Чему равны полное комплексное сопротивление контура, его активная и реактивная составляющие, как они меняются в окрестности резонансной частоты? 13.2. Каким выражением определяется комплексный коэффициент передачи параллельного колебательного контура? Чему равны его АЧХ и ФЧХ, как они отображаются графически? 13.3. Запишите формулы для резонансной частоты, резонансного и характеристического сопротивления, добротности и полосы пропускания контура. 13.4. Запишите в координатах обобщенной расстройки выражения для входного сопротивления, комплексного коэффициента передачи, АЧХ и ФЧХ параллельного колебательного контура. 13.5. Как отображаются графически в координатах обобщенной расстройки АЧХ и ФЧХ параллельного колебательного контура? 13.6. Как влияют внутреннее сопротивление источника сигнала и нагрузка на частотные характеристики контура? Каковы требования к величинам этих сопротивлений? 13.7. Запишите выражение для комплексного коэффициента передачи двух связанных контуров. Изобразите графики АЧХ и ФЧХ. Как влияют параметры контуров на форму частотных характеристик? 13.8. Как определяются коэффициент и фактор связи? Как зависит от них форма АЧХ?
ЗАДАЧИ
Задача 13.1 (2 балла). Применительно к параллельному колебательному контуру (рис.13.1, а) рассчитайте и изобразите графически зависимость сопротивления контура R=R1+R2=(5+G+N) Ом, L=(400+(-1)N · 5(N+G)) мкГн, C=(600-GN) пФ.
Обратите внимание на то, какой порядок имеет резонансное сопротивление параллельного контура, сопоставьте его с резонансным сопротивлением последовательного контура (тема 12). Рассчитайте и постройте кривую зависимости напряжения Uk на контуре (рис. 13.1, б) от расстройки J=(10+0, 1 (-1)N (N+G)) мА. Определите резонансное значение Uk0 амплитуды напряжения на контуре в вольтах и введите его в АКОС для проверки.
Вычисления проведите для двух значений сопротивления RJ, равных:
Присмотритесь к построенным кривым - как влияет внутреннее сопротивление источника сигнала на частотную избирательность цепи. Вычислите амплитуды резонансных напряжений Величину Задача 13.3 (2 балла). Определите коэффициент передачи по напряжению Рис. 13.3 R=(5+0, 01 NG) кОм. Значение 1000 H занесите в АКОС.
Параметры контура возьмите из задачи 13.1, величину RE - из задачи 13.3. Определите коэффициент включения контура
и введите значение 1000· Задача 13.5 (2 балла). Применительно к одиночному колебательному контуру (рис.13.5, а) и к системе из двух аналогичных связанных контуров (рис.13.5, б) при факторе связи A=1 рассчитайте и постройте зависимости
Вычисления проведите в диапазоне значений Примите индивидуально Q=80(1+(-1)NN/(15+N+G)).
Рис. 13.5
Сравните между собой по форме полученные характеристики с точки зрения избирательности. Какая из них обеспечивает большую равномерность коэффициента передачи в полосе пропускания и большее ослабление сигнала за ее пределами? Найдите при Величину 1000· Задача 13.6 (2 балла). Для системы из двух идентичных связанных контуров (рис.13.5, б) рассчитайте и постройте зависимость приведенного коэффициента передачи
A=(1, 3+0, 01 NG)
в том же масштабе, что и в задаче 13.5. Величину добротности возьмите из предыдущей задачи. Определите, чему равен коэффициент передачи
ТЕМА 14. ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХ- ПОЛЮСНИКОВ И ФИЛЬТРЫ
КОНТРОЛЬНЫЕ ВОПРОСЫ
14.1. Дайте определение четырехполюсника. Как он изображается графически, как задаются положительные направления токов и напряжений? 14.2. Какими системами параметров описывается четырехполюсник? 14.3. Запишите систему уравнений четырехполюсника для А-параметров. Как они определяются расчетным путем и экспериментально, каков их физический смысл? 14.4. Как выражаются через А-параметры комплексные коэффициенты передачи четырехполюсника по току и напряжению? 14.5. Дайте определение меры передачи (постоянной распространения) и затухания четырехполюсника. 14.6. Что представляют собой характеристические сопротивления четырехполюсника, как они выражаются через А-параметры? 14.7. Запишите системы уравнений четырехполюсника для Z, Y и H -параметров. Как они определяются расчетным путем и экспериментально, каков их физический смысл? 14.8. Что представляет собой частотный фильтр, какими свойствами он обладает? Приведите примеры различных типов частотных фильтров. 14.9. Рассмотрите сложные реактивные частотные фильтры, из каких звеньев они состоят? 14.10. Рассмотрите характеристики затухания простейших Т-образных реактивных звеньев ФНЧ и ФВЧ. Какими выражениями они определяются? 14.11. Как определяется частота среза реактивного Т-образного звена?
ЗАДАЧИ
14.1 (2 балла). В результате измерений (опытов холостого хода и короткого замыкания), выполненных на четырехполюснике (рис.14.1), получены данные, приведенные в таблице 14.1.
Рис.14.1
Если Ваш номер четный, исходя из опытных данных определите Y - параметры рассматриваемого четырехполюсника и составьте матрицу Y-параметров ||Y|| в форме
Вычислите модуль определителя матрицы |Y| (в миллисименсах в квадрате) и внесите его значение в АКОС для проверки. Если Ваш номер нечетный, исходя из опытных данных определите Z - параметры рассматриваемого четырехполюсника и составьте матрицу Z-параметров ||Z|| в форме
Вычислите модуль определителя матрицы Z –пара-метров (в килоомах в квадрате) и внесите его значение в АКОС для проверки.
R1 = 10 G Oм; Рис. 14.2 R2=(200+(-1)N3N) Ом; R3=(200+(-1)N3N) Ом; R4 = 10 G Ом. Вычислите определитель |Y| (в миллисименсах в квадрате) или |Z| (в омах в квадрате) и внесите его в АКОС для проверки. 14.3. (2 балла) Определите непосредственно по схеме цепи или по формулам пересчета одних параметров в другие (их можно найти в учебниках) А-параметры цепи (рис.14.2). Используя найденные значения А-параметров, получите расчетную формулу для определения входного сопротивления цепи Zвх при произвольной нагрузке RН. Для исходных данных из задачи 14.2 вычислите входное сопротивление цепи при следующем значении RН:
RН = (400 + (-1)N 10 N + 10 G) Ом.
Внесите полученное значение Zвх (в омах) в АКОС для проверки. 14.4. (2 балла) Определите методом теории четырехполюсников коэффициент передачи цепи (рис.14.2) по ее А-параметрам. Найдите напряжение на нагрузке U2 при следующих данных:
U1 = (20 G + 10 N) B, Rн = (200 + 3 N) Ом, (N-четное);
U1 = (100 - 2 N) B, Rн = (100 + 10 N G) Ом, (N-нечетное).
Данные цепи возьмите из задачи 14.2. Полученное значение U2 в вольтах введите в АКОС. 14.5. (2 балла) Применительно к Т-образному симметричному четырехполюснику (рис.14.3а), если Ваш номер четный, и к П-образному симметричному четырехполюснику (рис.14.3б), если номер нечетный, определите, при каком сопротивлении нагрузки Z2=ZС входное сопротивление четырехполюсника ZВХ=ZС, ZС – характеристическое сопротивление четырехполюсника. Примите
|

 = 5 G В,
= 5 G В, = (20 + (-1)N 2 G) В,
= (20 + (-1)N 2 G) В,  = 0, 5 G А.
= 0, 5 G А. в миллиамперах внесите в АКОС.
в миллиамперах внесите в АКОС. 10.6. (2 балла). Для цепи рис.10.13 составьте систему уравнений по методу узловых потенциалов и решите ее относительно тока
10.6. (2 балла). Для цепи рис.10.13 составьте систему уравнений по методу узловых потенциалов и решите ее относительно тока  через диагональную ветвь G12 при следующих данных:
через диагональную ветвь G12 при следующих данных: = (6 G + 2 N) В.
= (6 G + 2 N) В. в миллиамперах занесите в АКОС.
в миллиамперах занесите в АКОС.

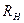 на свойства фильтра нижних частот, показанного на рис. 11.2. Постройте графики АЧХ для различных
на свойства фильтра нижних частот, показанного на рис. 11.2. Постройте графики АЧХ для различных 

 Выведите расчетное соотношение для определения амплитудно-частотной характеристики (АЧХ) по напряжению
Выведите расчетное соотношение для определения амплитудно-частотной характеристики (АЧХ) по напряжению  применительно к отобранной Вами схеме цепи. Расcчитайте и постройте (в масштабе) график зависимости H(ω) в диапазоне частот от ω =0 до такого значения переменной ω, при котором функция H(ω) будет мало меняться.
применительно к отобранной Вами схеме цепи. Расcчитайте и постройте (в масштабе) график зависимости H(ω) в диапазоне частот от ω =0 до такого значения переменной ω, при котором функция H(ω) будет мало меняться. ,
, и введите его в АКОС.
и введите его в АКОС. Задача 11.6 (3 балла). Определите, чему равно проходное сопротивление цепи рис. 11.6
Задача 11.6 (3 балла). Определите, чему равно проходное сопротивление цепи рис. 11.6
 кОм,
кОм, .
. Задача 12.2 (2 балла). Рассчитайте и постройте амплитудно-частотную характеристику контура H(Δ ω) при данных из предыдущей задачи. Вычислите и определите по графику полосу пропускания контура П, сопоставьте результаты. Определите наибольшее значение частоты ω max (килорадиан делить на секунду) на границе полосы пропускания контура и введите его в АКОС.
Задача 12.2 (2 балла). Рассчитайте и постройте амплитудно-частотную характеристику контура H(Δ ω) при данных из предыдущей задачи. Вычислите и определите по графику полосу пропускания контура П, сопоставьте результаты. Определите наибольшее значение частоты ω max (килорадиан делить на секунду) на границе полосы пропускания контура и введите его в АКОС. напряжения мешающей радиостанции по сравнению с полезной на выходе контура
напряжения мешающей радиостанции по сравнению с полезной на выходе контура ,
, Задача 12.5 (2 балла). На колебательный контур воздействуют
Задача 12.5 (2 балла). На колебательный контур воздействуют от расстройки
от расстройки  , где
, где  - резонансная частота контура, при следующих исходных данных:
- резонансная частота контура, при следующих исходных данных:
 Рис. 13.1
Рис. 13.1 при подключении к нему идеального источника тока с амплитудой
при подключении к нему идеального источника тока с амплитудой Задача 13.2 (2 балла). Рассчитайте и постройте график зависимости амплитуды напряжения Uk на контуре (рис. 13.2) от расстройки
Задача 13.2 (2 балла). Рассчитайте и постройте график зависимости амплитуды напряжения Uk на контуре (рис. 13.2) от расстройки  =(G/4(N+G))·(L/RC),
=(G/4(N+G))·(L/RC), =(3/G(N+3))·(L/RC).
=(3/G(N+3))·(L/RC). и
и  на контуре при двух указанных значениях RJ.
на контуре при двух указанных значениях RJ. введите в АКОС-1.
введите в АКОС-1. цепи рис. 13.3 на резонансной частоте при питании параллельного контура с параметрами, указанными в задаче 13.1, от источника гармонической ЭДС с амплитудой E и внутренним сопротивлением, равным
цепи рис. 13.3 на резонансной частоте при питании параллельного контура с параметрами, указанными в задаче 13.1, от источника гармонической ЭДС с амплитудой E и внутренним сопротивлением, равным Задача 13.4 (2 балла). В сложном параллельном контуре рис. 13.4 укажите, как следует разделить общую индуктивность L между ветвями (L1 и L2), чтобы согласовать его резонансное сопротивление
Задача 13.4 (2 балла). В сложном параллельном контуре рис. 13.4 укажите, как следует разделить общую индуктивность L между ветвями (L1 и L2), чтобы согласовать его резонансное сопротивление  с сопротивлением источника RE для обеспечения передачи максимальной мощности от источника в контур.
с сопротивлением источника RE для обеспечения передачи максимальной мощности от источника в контур.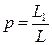
 в АКОС для проверки.
в АКОС для проверки. , где h - приведенный коэффициент передачи контура по напряжению, определяемый равенством
, где h - приведенный коэффициент передачи контура по напряжению, определяемый равенством ,
, - относительная расстройка, равная
- относительная расстройка, равная ,
,
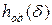 и связанных контуров
и связанных контуров  и их отношение
и их отношение  .
. введите в АКОС.
введите в АКОС.
 В
В
 В
В
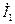 мА
мА
 мА
мА
 ,
,  .
. ,
, 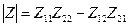 .
.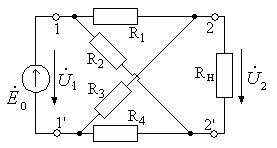 14.2. (2 балла) Если Ваш номер нечетный, найдите расчетным путем Y-параметры мостового (рис.14.2) четырехполюсника, а если четный - найдите его Z-параметры при следующих данных:
14.2. (2 балла) Если Ваш номер нечетный, найдите расчетным путем Y-параметры мостового (рис.14.2) четырехполюсника, а если четный - найдите его Z-параметры при следующих данных:


