ВВЕДЕНИЕ 8 страница
Z1 = (30 + (-1)N 0.5 N) Ом, Z2 = (90 + 5 G + N) Ом. Найденные значения ZС в омах внесите в АКОС.
Рис.14.3
14.6. (2 балла). При четном N определите граничную частоту L1 = 0.01 N G Гн, L2 = (0.5 + 0.05 N G) Гн. С1 = (300 + (-1) (N + G) нФ, С2 = (N + G) мкФ,
Рис. 14.4
Рассчитайте и постройте в масштабе характеристику затухания фильтра a = (W/Wср). Определите значения затухания фильтра a1 (децибел) и a2 (децибел) на частотах:
W/Wср =1+0.001G N, W/Wср =1.4 - 0.01(N + G) для четных N, W/Wср = 0.9 + 0.002 N, W/Wср = 1 - 0.01 G для нечетных N,
сложите их и a = 10 (a1 + a2) внесите в АКОС для проверки. ТЕМА 18. ЧАСТОТНЫЕ СПЕКТРЫ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
КОНТРОЛЬНЫЕ ВОПРОСЫ
18.1. Запишите выражения для ряда Фурье и коэффициентов разложения периодического сигнала. Дайте определение спектров амплитуд и фаз. 18.2. Определите спектры амплитуд и фаз периодической последовательности прямоугольных импульсов, постройте их графики. 18.3. Как влияют на спектры амплитуд амплитуда, длительность и период последовательности прямоугольных импульсов? 18.4. Запишите ряд Фурье в комплексной форме и формулы для вычисления коэффициентов разложения. Как определяются комплексные амплитуды гармоник сигнала? 18.5. Определите комплексные амплитуды гармоник периодической последовательности прямоугольных импульсов. Как определяются при этом спектры амплитуд и фаз? 18.6. Сформулируйте теорему запаздывания. Как влияет временная задержка сигнала на его спектры амплитуд и фаз? 18.7. Как сказывается на спектральных свойствах сигнала его симметрия (четность или нечетность), как можно практически использовать эти результаты? 18.8. Что представляет собой ширина спектра сигнала, как она определяется, что характеризует? Как влияют на ширину спектра параметры прямоугольных импульсов? Каковы инженерные оценки ширины спектра импульсных сигналов? 18.9. Как в инженерной практике может использоваться ширина спектра сигнала? Как она должна соотноситься с полосой пропускания тракта обработки сигнала?
ЗАДАЧИ 18.1. (1 балл). Дано гармоническое колебание, определяемое выражением u(t)=Ucos(
Результат в АКОС не вводится, а предъявляется для проверки преподавателю на практическом занятии. 18.2. (1 балл). Определите путем простого тригонометрического преобразования, на какие составляющие (спектр амплитуд) можно расчленить колебание (рис.18.1), выражаемое равенством u(t)= U cos2( при данных задачи 18.1. Колебание образуется при возведении гармонической функции в квадрат, что в радиотехнических цепях и автоматике достигается посредством электронных устройств.
18.3. (3 балла). Найдите, воспользовавшись формулами Фурье, выражения для определения постоянной составляющей и амплитуд гармоник одного из процессов, представленных на рис.18.2, в соответствии с Вашим номером N.
Определите численно по найденным Вами выражениям постоянную составляющую и амплитуды восьми первых гармонических составляющих процесса. Представьте спектр амплитуд в графическом виде.
Рис.18.2а
Рис.18.2б
Рис.18.2в
Рис.18.2г
Рис.18.2д
Рис.18.2е
Рис.18.2ж
Рис.18.2з
Параметры сигнала примите равными:
Вычислите с проверочной целью сумму амплитуд второй и третьей гармоник (в амперах) S=I2+I3 и внесите эту величину для проверки в АКОС. 18.4 (3 балла). Найдите выражение для спектра амплитуд колебания треугольной (пилообразной) формы на рис.18.3:
для N= 1, 2, 5, 6, 9, 10, 13, 14, 17, 18, 21, 22, 25, 26, 29, 30
Рис.18.3а
для N= 3, 4, 7, 8, 11, 12, 15, 16, 19, 20, 23, 24, 27, 28, 31, 32
Рис.18.3б
Представьте спектр амплитуд в графическом виде при следующих данных: I = (2 N + 3 G) А, T = (N + 3) мс. Определите суммарную мощность постоянной составляющей и первых двух гармоник, P = P0 + P1 + P2, в предположении, что ток течет через сопротивление 1 Ом. Значение Р в ваттах введите в АКОС. 18.5. (2 балла). Отберите в соответствии с Вашим номером N одно из двух колебаний прямоугольной формы, представленных на рис.18.4, а, б, при следующих данных: E = 12 В, T = 1 с,
При четном N
Рис.18.4а
При нечетном N
Рис.18.4б Положим, что это колебание подается на вход идеального фильтра нижних частот с равномерной амплитудно-частотной характеристикой H( Определите и представьте в графическом виде спектры амплитуд колебаний на входе и на выходе фильтра при его граничной частоте
Рис.18.6
Укажите, чему равна амплитуда крайней справа, прошедшей через фильтр гармонической составляющей и внесите ее значение (в милливольтах) для проверки в АКОС. 18.6 (2 балла). Напишите выражение для спектральной плотности процесса (рис.18.5) из задачи 18.5. Нанесите кривую спектральной плотности на бумагу в том масштабе по оси частот, который был выбран в предыдущей задаче при изображении спектров. Найдите спектральную плотность F(
ТЕМА 19. ЧАСТОТНЫЕ СПЕКТРЫ НЕПЕРИОДИЧЕСКИХ ПРОЦЕССОВ КОНТРОЛЬНЫЕ ВОПРОСЫ
19.1. Почему нельзя описывать спектры непериодических сигналов с помощью ряда Фурье? 19.2. Запишите прямое и обратное преобразования Фурье. Как осуществляется переход от ряда Фурье к преобразованию Фурье? Каков физический смысл полной комплексной спектральной плотности? 19.3. Как определяя плотность амплитуд и спектр фаз непериодического сигнала, каков их физический смысл и размерность?
19.5. Рассмотрите пример расчета спектров амплитуд и фаз одиночного прямоугольного импульса, показанного на рис. 19.1. Постройте их графики. 19.6. Как определяется ширина спектра одиночного импульса? Как проводится инженерная оценка его ширины спектра? Рис. 19.1
ЗАДАЧИ 19.1. (2 балла). Спектр импульса прямоугольной формы (рис.19.2, а), определяется комплексной спектральной плотностью
где Модуль и аргумент спектральной плотности выражаются равенствами:
где
Рис.19.2
Зависимости их значений от частоты приведены в графическом виде на рис.19.3.
Рис.19.3
Воспользовавшись теоремой смещения, определите комплексную спектральную плотность Величину Найдите модуль и аргумент спектральной плотности смещенного импульса e2(t) (рис.19.2б), представьте их в графическом виде, подобно рис.19.3, и сопоставьте полученные результаты. Зафиксируйте с необходимыми объяснениями, какие изменения произошли в спектрах за счет смещения импульса во времени. Определите в интервале от 0 до 2 19.2. (2 балла). Увеличьте длительность (ширину) импульса (рис.19.2а) в Рассчитайте и постройте кривую спектральной плотности амплитуд Определите значение спектральной плотности амплитуд расширенного импульса на частоте 19.3. (2 балла). Найдите, воспользовавшись теоремой сложения, комплексную спектральную плотность п а р ы импульсов (рис.19.4) с параметрами, указанными для первого и второго импульсов в задаче 19.1 (рис.19.2а и рис.19.2б соответственно). Представьте функцию 19.4. (2 балла). Определите спектральную плотность одного из импульсов экспоненциальной формы (рис.19.5) в зависимости от Вашего N при I = (0, 1 G) А, d = 1000 G 1/с. N = 1 – 8 N = 9 – 16
Рис.19.5а Рис.19.5б
N = 17 – 24 N = 25 – 31
Рис.19.5в Рис.19.5г
Постройте график Найдите значение спектральной плотности энергии 19.5. (2 балла). Определите, исходя из спектральной плотности энергии Найдите полосу частот (ширину спектра) Ш, в которой сосредоточено (80+0, 3N) процентов энергии импульса. Значение 0, 03× Ш в радианах, деленных на секунду, внесите для проверки в АКОС. 19.6. (2 балла). Найдите спектральным методом напряжение u2(t) на выходе цепи (рис.19.6, б) при скачкообразном возрастании напряжения u1(t) на ее входе от 0 до Е (рис.19.6, а). Такого рода ступенчатая функция u1(t) на входе цепи наблюдается при включении источника постоянной ЭДС и называется соответственно функцией включения. Аналитически ее записывают следующим образом:
Комплексная спектральная плотность функции включения u1(t) определяется равенством F1(j
Рис.19.5
Определите комплексный коэффициент передачи цепи. С помощью обратного преобразования Фурье найдите выходное напряжение цепи u2(t)=uС(t) при четном N или u2(t)=uR(t) при нечетном N.
Справка:
Рассчитайте и постройте кривую u2(t) при следующих значениях параметров цепи:
Е = 30 В, R = 1 кОм, L = 1 мГн, C = 1 нФ.
Найдите значение напряжения u2(t) в милливольтах на выходе цепи в момент времени t=(0, 5 N + 2 G)/40 мкс и внесите его в АКОС для проверки.
ТЕМА 20. СВОБОДНЫЕ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ ПЕРВОГО ПОРЯДКА
КОНТРОЛЬНЫЕ ВОПРОСЫ
20.2. Сформулируйте законы Ома и Кирхгофа для мгновенных значений сигналов. Приведите пример формирования дифференциального уравнения цепи для цепи, показанной на рис. 19.1..
Рис. 20.1
20.3. Сформулируйте законы коммутации. Из каких соображений они вытекают, для чего используются? 20.4. Как определяются начальные условия переходного процесса? Приведите пример для цепи рис. 20.1. 20.5. Изложите общую методику решения однородного и неоднородного дифференциальных уравнений. 20.6. Как определяется свободная составляющая переходного (свободного) процесса? 20.7. Как определяется принужденная составляющая переходного процесса? 20.8. Исходя из чего определяются постоянные интегрирования дифференциального уравнения?
ЗАДАЧИ
20.1 (2 балла). В схеме рис.20.2 установите ключи в положения, соответствующие Вашему номеру N в списке группы, записанному в двоичной форме. Таблица перевода десятичных чисел в двоичные приведена в конце руководства. Перечертите получившуюся схему в свою тетрадь. Ключ К5 указывает, что требуется определить студенту в данной задаче: ток в цепи i(t) или напряжение u(t) на элементе с индексом 2. Значения сопротивлений, емкостей, индуктивностей и данные источников примите равными: Re= 2 кОм, Ri = 1 кОм, R1 = 2 (3 + (-1)N)/G кОм, R2 = (3 - (-1)N)/G кОм, C1 = (1 + N/20) мкФ, C2 = (4 - N/20) мкФ, L1 = (G + 3) Гн, L2 = (5 + N/10) Гн.
Рис.20.2 Предположите, что источник постоянной ЭДС e0(t)=E0 или источник постоянного тока i0(t)=I0 в момент t=0 выключился, как это изображено на диаграммах (рис.20.3а и б).
Рис. 20.3
Примите: E0=(15 + (-1)N G) В, I0=(15 - (-1)N G) мА. В цепи возникает свободный процесс за счет энергии, накопленной в индуктивности или емкости. 1. Определите начальные условия - ток через индуктивность или напряжение на емкости при t=0. 2. Составьте дифференциальное уравнение цепи и найдите его общее решение применительно к i(t) или u(t) с конкретными данными Вашей цепи. 3. Получите выражения для процессов i(t) или u(t) в зависимости от положения ключа К5. 4. Представьте процесс i(t) или u(t) в графическом виде в масштабе, построив его " по точкам". 5. Найдите значение тока i(t=t1) в микроамперах или напряжения u(t=t1) в милливольтах при t1=(100N + 200G) мкс. Внесите значение i(t1) или u(t1) в АКОС для проверки. 20.2. (1 балл). Вычислите постоянную времени Вашей цепи Задача 20.3. (3 балла). Определите переходной процесс i(t) или u(t) в цепи (рис.20.2) в соответствии с положением К5 при включении источника ЭДС или тока в момент t=0, как показано на рис.20.4, при нулевых начальных условиях. Значения параметров цепи возьмите из задачи 20.1.
Рис.20.4
Представьте процесс в графическом виде, построив его в масштабе по точкам. Найдите значения i(t=t2) или u(t=t2) при t2=t1 из задачи 20.1 Отметьте точку на чертеже. Внесите значения i(t2) в микроамперах или u(t2) в милливольтах в АКОС для проверки. 20.4 (3 балла). Определите, используя полученные выше результаты, какой вид имеет ток i(t) или напряжение на выходе цепи u(t) при воздействии на цепь импульса ЭДС e0(t) или тока i0(t) длительностью tu=t1=(100N + 200G) мкс, показанного на рис.20.5, а, б.
Рис.20.5 Представьте импульсы i(t) и u(t) в графической форме. Найдите значения i(t=t3) в микроамперах или u(t=t3) в милливольтах при t3 = 2t1. Значение i(t3) или u(t3) (в зависимости от положения ключа К5) внесите в АКОС для проверки. Задачу решите методом сложения реакций цепи на включение (в момент t=0) и выключение источника (в момент t = tu), то есть представив импульс рис.20.5 в виде суммы двух сигналов s1t) и s2(t), показанных на рис.20.6.
Рис.20.6
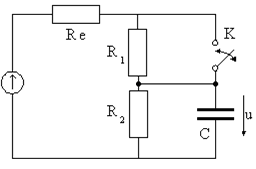
20.5 (2 балла). Определите, по какому закону будет изменяться напряжение на конденсаторе uC(t) в цепи (рис.20.7), подсоединенной к источнику постоянной ЭДС Е = (30 - 2 G) В, при замыкании (для четных N) или размыкании (для нечетных N) ключа К для следующих данных цепи:
Re = 1 кОм, R1= (6 + G - N/8) кОм, R2= (G + N/2) кОм, C = (10 - N/5) мкФ.
Рис. 20.7
Представьте результат в графическом виде. Для решения задачи необходимо найти начальное значение напряжения на конденсаторе uC(0) до коммутации и определить закон изменения напряжения на нем после коммутации с учетом постоянной времени цепи после коммутации. Определите напряжение на конденсаторе в момент t4=t1 из задачи 20.1 и занесите значение u(t4=t1) в милливольтах для проверки в АКОС. Задача 20.6 (1 балл). Конденсатор емкостью С = 5 G мкФ, заряженный до напряжения 40 кВ, разряжается через сопротивление R = (12 + (-1)N× N/5) МОм в цепи рис.20.7. Определите время Т, через которое конденсатор разрядится до безопасного для человека напряжения, равного 36 В. Значение Т в секундах введите в АКОС.
Рис.20.8
ТЕМА 21. СВОБОДНЫЕ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
КОНТРОЛЬНЫЕ ВОПРОСЫ
21.1. Какие режимы свободных колебаний могут возникать в последовательном колебательном контуре? При каких условиях они возникают? Как это связано с корнями характеристического уравнения? 21.2 Изобразите временные диаграммы свободных процессов в колебательном контуре в каждом из режимов. 21.3. Каким выражением определяется частота свободных колебаний? Как она зависит от параметров колебательного контура r, L, C? 21.4. По какому закону изменяется амплитуда свободных колебаний в контуре? Чему равен коэффициент затухания? 21.5. Как определяется декремент затухания и логарифмический декремент затухания? Как они зависят от параметров контура? 21.6. Как определяются коэффициент затухания и логарифмический декремент затухания экспериментально по осциллограмме?
|


 (частоту среза) реактивного фильтра нижних частот (рис.14.4а), а при нечетном N - граничную частоту фильтра верхних частот (рис.14.4б) при следующих данных:
(частоту среза) реактивного фильтра нижних частот (рис.14.4а), а при нечетном N - граничную частоту фильтра верхних частот (рис.14.4б) при следующих данных:
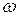 t-
t-  ). Изобразите это колебание в масштабе посредством двух спектральных линий U(
). Изобразите это колебание в масштабе посредством двух спектральных линий U( (15 + 2 N +2 G) рад/с,
(15 + 2 N +2 G) рад/с, Найдите и представьте спектр амплитуд данного колебания в графическом виде путем разложения его на составляющие. Значения частоты
Найдите и представьте спектр амплитуд данного колебания в графическом виде путем разложения его на составляющие. Значения частоты 

















 = 0, 2 T.
= 0, 2 T.




 (N + G) рад/с и внесите ее для проверки в АКОС.
(N + G) рад/с и внесите ее для проверки в АКОС. 19.4. Опишите влияние симметрии сигнала на свойства полной комплексной спектральной плотности, спектров амплитуд и фаз.
19.4. Опишите влияние симметрии сигнала на свойства полной комплексной спектральной плотности, спектров амплитуд и фаз.

 - целое число.
- целое число.


 Первая кривая показывает, как зависит от частоты спектральная плотность а м п л и т у д, вторая - спектр ф а з импульса рис.19.2а.
Первая кривая показывает, как зависит от частоты спектральная плотность а м п л и т у д, вторая - спектр ф а з импульса рис.19.2а.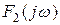 импульса (рис.19.2б), сдвинутого на
импульса (рис.19.2б), сдвинутого на 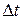 относительно исходного.
относительно исходного. импульса e2(t) на частоте
импульса e2(t) на частоте  для импульса длительностью
для импульса длительностью  , где
, где  в графическом виде. Определите значение
в графическом виде. Определите значение 







 . Рассчитайте и постройте кривую зависимости спектральной плотности э н е р г и и
. Рассчитайте и постройте кривую зависимости спектральной плотности э н е р г и и  от частоты. Поместите графики
от частоты. Поместите графики  для удобства сравнения один под другим при одинаковом масштабе по оси абсцисс.
для удобства сравнения один под другим при одинаковом масштабе по оси абсцисс.