Матрица парных коэффициентов корреляций
Анализ матрицы парных коэффициентов корреляции показывает, что результативный показатель наиболее тесно связан с показателем x (4) — количество удобрений, расходуемых на 1 га ( В то же время связь между признаками-аргументами достаточно тесная. Так, существует практически функциональная связь между числом колесных тракторов (x (1)) и числом орудий поверхностной обработки почвы О наличии мультиколлинеарности свидетельствуют также коэффициенты корреляции Чтобы продемонстрировать отрицательное влияние мультиколлинеарности, рассмотрим регрессионную модель урожайности, включив в нее все исходные показатели:
(1.8)
В скобках указаны значения исправленных оценок среднеквадратических отклонений оценок коэффициентов уравнения Под уравнением регрессии представлены следующие его параметры адекватности: множественный коэффициент детерминации Уравнение регрессии значимо, т.к. Fнабл = 121 > Fkp = 2, 85 найденного по таблице F -распределения при a=0, 05; n1=6 и n2=14. Из этого следует, что Q¹ 0, т.е. и хотя бы один из коэффициентов уравнения q j (j = 0, 1, 2,..., 5) не равен нулю. Для проверки гипотезы о значимости отдельных коэффициентов регрессии H0: qj=0, где j =1, 2, 3, 4, 5, сравнивают критическое значение t kp = 2, 14, найденное по таблице t -распределения при уровне значимости a=2 Q =0, 05 и числе степеней свободы n=14, с расчетным значением Не поддаются экономической интерпретации отрицательные знаки коэффициентов регрессии при x (1) и x (5). Из отрицательных значений коэффициентов следует, что повышение насыщенности сельского хозяйства колесными тракторами (x (1)) и средствами оздоровления растений (x (5)) отрицательно сказывается на урожайности. Таким образом, полученное уравнение регрессии неприемлемо. Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа. Первоначально используем пошаговый алгоритм с исключением переменных. Исключим из модели переменную x (1), которой соответствует минимальное по абсолютной величине значение ½ t 1½ =0, 01. Для оставшихся переменных вновь построим уравнение регрессии:
Полученное уравнение значимо, т.к. Fнабл = 155 > Fkp = 2, 90, найденного при уровне значимости a=0, 05 и числах степеней свободы n1=5 и n2=15 по таблице F -распределения, т.е. вектор q¹ 0. Однако в уравнении значим только коэффициент регрессии при x (4). Расчетные значения ½ t j½ для остальных коэффициентов меньше t кр = 2, 131, найденного по таблице t -распределения при a=2 Q =0, 05 и n=15. Исключив из модели переменную x (3), которой соответствует минимальное значение t 3=0, 35 и получим уравнение регрессии:
В полученном уравнении статистически не значим и экономически не интерпретируем коэффициент при x (5). Исключив x (5) получим уравнение регрессии:
Мы получили значимое уравнение регрессии со значимыми и интерпретируемыми коэффициентами. Однако полученное уравнение является не единственно “хорошей” и не “самой лучшей” моделью урожайности в нашем примере. Покажем, что в условии мультиколлинеарности пошаговый алгоритм с включением переменных является более эффективным. На первом шаге в модель урожайности y входит переменная x (4), имеющая самый высокий коэффициент корреляции с y, объясняемой переменной - r (y, x (4))=0, 58. На втором шаге, включая уравнение наряду с x (4) переменные x (1) или x (3), мы получим модели, которые по экономическим соображениям и статистическим характеристикам превосходят (1.10):
и
Включение в уравнение любой из трех оставшихся переменных ухудшает его свойства. Смотри, например, уравнение (1.9). Таким образом, мы имеем три “хороших” модели урожайности, из которых нужно выбрать по экономическим и статистическим соображениям одну. По статистическим критериям наиболее адекватна модель (1.11). Ей соответствуют минимальные значения остаточной дисперсии Несколько худшие показатели адекватности имеет модель (1.12), а затем — модель (1.10). Будем теперь выбирать наилучшую из моделей (1.11) и (1.12). Эти модели отличаются друг от друга переменными x (1) и x (3). Однако в моделях урожайностей переменная x (1) (число колесных тракторов на 100 га) более предпочтительна, чем переменная x (3) (число орудий поверхностной обработки почвы на 100 га), которая является в некоторой степени вторичной (или производной от x (1)). В этой связи из экономических соображений предпочтение следует отдать модели (1.12). Таким образом, после реализации алгоритма пошагового регрессионного анализа с включением переменных и учета того, что в уравнение должна войти только одна из трех связанных переменных (x (1), x (2) или x (3)) выбираем окончательное уравнение регрессии:
Уравнение значимо при a=0, 05, т.к. Fнабл = 266 > Fkp = 3, 20, найденного по таблице F -распределения при a= Q =0, 05; n1=3 и n2=17. Значимы и все коэффициенты регрессии Из уравнения регрессии следует, что увеличение на единицу числа тракторов на 100 га пашни (при фиксированном значении x (4)) приводит к росту урожайности зерновых в среднем на 0, 345 ц/га. Приближенный расчет коэффициентов эластичности э1»0, 068 и э2»0, 161 показывает, что при увеличении показателей x (1) и x (4) на 1% урожайность зерновых повышается в среднем соответственно на 0, 068% и 0, 161%. Множественный коэффициент детерминации В нашем примере, по урожайности наиболее эффективно растениеводство ведется в районе, которому соответствует d 7 =28%, где урожайность на 28% выше средней по региону, и наименее эффективно — в районе с d 20 =-27, 3%.
|

 ).
). .
.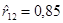 и
и 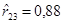 . Учитывая тесную взаимосвязь показателей x (1), x (2) и x (3), в регрессионную модель урожайности может войти лишь один из них.
. Учитывая тесную взаимосвязь показателей x (1), x (2) и x (3), в регрессионную модель урожайности может войти лишь один из них.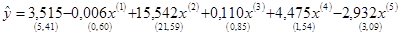
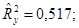

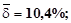 Fнабл = 121.
Fнабл = 121.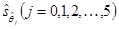 .
. ; исправленная оценка остаточной дисперсии
; исправленная оценка остаточной дисперсии  , средняя относительная ошибка аппроксимации
, средняя относительная ошибка аппроксимации 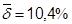 и расчетное значение
и расчетное значение 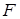 -критерия Fнабл = 121.
-критерия Fнабл = 121.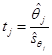 . Из уравнения следует, что статистически значимым является коэффициент регрессии только при x (4), так как ½ t 4½ =2, 90 > t kp=2, 14.
. Из уравнения следует, что статистически значимым является коэффициент регрессии только при x (4), так как ½ t 4½ =2, 90 > t kp=2, 14.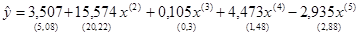
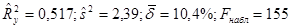
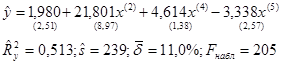 (1.9)
(1.9) (1.10)
(1.10)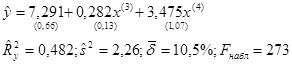 (1.11)
(1.11) (1.12)
(1.12) =2, 26 и средней относительной ошибки аппроксимации
=2, 26 и средней относительной ошибки аппроксимации  и наибольшие значения
и наибольшие значения 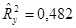 и Fнабл = 273.
и Fнабл = 273.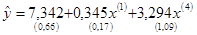
 и
и  в уравнении ½ t j½ > t kp(a=2 Q =0, 05; n=17)=2, 11. Коэффициент регрессии q1 следует признать значимым (q1¹ 0) из экономических соображений, при этом t 1=2, 09 лишь незначительно меньше t kp = 2, 11.
в уравнении ½ t j½ > t kp(a=2 Q =0, 05; n=17)=2, 11. Коэффициент регрессии q1 следует признать значимым (q1¹ 0) из экономических соображений, при этом t 1=2, 09 лишь незначительно меньше t kp = 2, 11.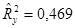 свидетельствует о том, что только 46, 9% вариации урожайности объясняется вошедшими в модель показателями (x (1) и x (4)), то есть насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (x (2), x (3), x (5), погодные условия и др.). Средняя относительная ошибка аппроксимации
свидетельствует о том, что только 46, 9% вариации урожайности объясняется вошедшими в модель показателями (x (1) и x (4)), то есть насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (x (2), x (3), x (5), погодные условия и др.). Средняя относительная ошибка аппроксимации 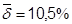 характеризует адекватность модели, так же как и величина остаточной дисперсии
характеризует адекватность модели, так же как и величина остаточной дисперсии 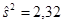 . При интерпретации уравнения регрессии интерес представляют значения относительных ошибок аппроксимации
. При интерпретации уравнения регрессии интерес представляют значения относительных ошибок аппроксимации 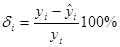 . Напомним, что
. Напомним, что 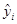 — модельное значение результативного показателя, характеризует среднее для совокупности рассматриваемых районов значение урожайности при условии, что значения объясняющих переменных x (1) и x (4) зафиксированы на одном и том же уровне, а именно x (1) = xi (1) и x (4) = xi (4). Тогда по значениям d i можно сопоставлять районы по урожайности. Районы, которым соответствуют значения d i > 0, имеют урожайность выше среднего, а d i < 0 — ниже среднего.
— модельное значение результативного показателя, характеризует среднее для совокупности рассматриваемых районов значение урожайности при условии, что значения объясняющих переменных x (1) и x (4) зафиксированы на одном и том же уровне, а именно x (1) = xi (1) и x (4) = xi (4). Тогда по значениям d i можно сопоставлять районы по урожайности. Районы, которым соответствуют значения d i > 0, имеют урожайность выше среднего, а d i < 0 — ниже среднего.


