Регрессионная модель среднедушевых сбережений при гетероскедастичности остатков
В табл.2.1 представлены данные (в млн. руб.) о среднедушевых сбережениях (y) и доходах (x) в n =10 семьях. Требуется построить две линейные регрессионные модели, характеризующие зависимость денежных сбережений (y) от среднедушевых доходов (x), соответственно, при соблюдении исходных предпосылок классической регрессионной модели и гетероскедастичности случайных регрессионных остатков. Сравнить точность оценок параметров q 0 и q 1 моделей. Таблица 2.1.
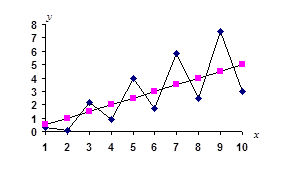
Решение. Предварительно представим наши данные графически. На рис. 2.1 представлены на плоскости все наши n =10 наблюдений, а также график линейного уравнения регрессии
Рис.2.1. Данные о среднедушевых сбережениях (y) и доходах (x) Из графика следует правомерность выбора линейной регрессионной модели вида: yi = q0 + q1xi + ei, i = 1, 2,..., n (2.1) Здесь подлежащий оцениванию вектор неизвестных коэффициентов уравнения имеет вид а) При построении классической линейной регрессионной модели предполагается, что случайные остатки ei независимы, нормальны и гомоскедастичны, т.е. ei Î N(0, s 2) и М eiej= 0 при i ¹ j и i, j = 1, 2,..., n. В случае классической регрессионной модели МНК-оценка
где для нашего примера
тогда
и
Тогда оценка уравнения регрессии имеет вид:
Найдем несмещенную оценку остаточной дисперсии:
откуда несмещенная оценка среднеквадратического отклонения равна Оценку ковариационной матрицы вектора
Таким образом, имеем исправленные оценки дисперсии элементов вектора б) Перейдем к построению линейного регрессионного уравнения в предположении гетероскедастичности случайных регрессионных остатков. На рис.2.1 хорошо видно, что с ростом доходов (х) вариация, размах отклонений сбережений (у) от линии регрессии ( Пусть регрессионная модель имеет вид: yi = q0 + q1 xi + Предполагается, что В случае модели (2.3) оценку векторов параметров q* = (X T V -1 X)-1 X T V -1Y (2.4) где
Поясним алгоритм нахождения оценок (2.4) для нашей двумерной модели (1.3). Разделив левую и правую части уравнения (2.3) на xi, получим:
Относительно новых переменных
параметры которой оцениваются с помощью МНК. МНК-оценка уравнения регрессии имеет вид:
Окончательно уравнение регрессии можно записать:
Уравнение обладает следующими статистическими характеристиками: Сравним статистические характеристики уравнений регрессий, полученных с помощью МНК (2.2) и ОМНК (2.5). Второе уравнение имеет более точные оценки элементов вектора q, а именно: Таким образом, в нашем примере ОМНК-оценки коэффициентов уравнения q0 и q1 оказались точнее, эффективнее.
|

 .
.
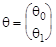
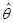 вектора qопределяется из выражения:
вектора qопределяется из выражения: ,
,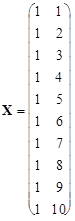 ;
; 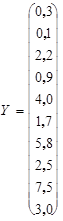
 ;
;  ;
; 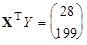 .
.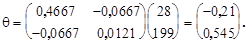
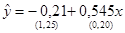 (2.2)
(2.2)
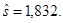
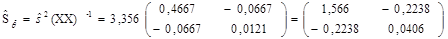
 и
и 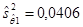 . Отсюда находим среднеквадратические отклонения, значения которых приведены в скобках под уравнением регрессии (2.2).
. Отсюда находим среднеквадратические отклонения, значения которых приведены в скобках под уравнением регрессии (2.2). ) растет пропорционально х, что свидетельствует о гетероскедастичности случайных остатков, т.е., что e*=e× х.
) растет пропорционально х, что свидетельствует о гетероскедастичности случайных остатков, т.е., что e*=e× х. , где i =1, 2,..., n (2.3)
, где i =1, 2,..., n (2.3) ) и М
) и М 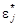 =0 при i ¹ j и i, j= 1, 2,..., n.
=0 при i ¹ j и i, j= 1, 2,..., n.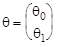 находят с помощью обобщенного МНК. ОМНК - оценка вектора q равна:
находят с помощью обобщенного МНК. ОМНК - оценка вектора q равна:
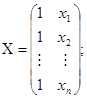
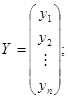

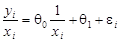 .
.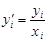 и
и 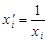 мы имеем классическую регрессионную модель
мы имеем классическую регрессионную модель
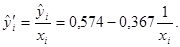
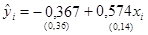 (2.5)
(2.5) ;
; 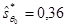 ;
; 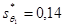 .
.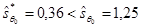 и
и 



